stl2vec: Semantic and Interpretable Vector Representation of Temporal Logic

Integrating symbolic knowledge and data-driven learning algorithms is a longstanding challenge in Artificial Intelligence. Despite the recognized importance of this task, a notable gap exists due to the discreteness of symbolic representations and the continuous nature of machine-learning computations. One of the desired bridges between these two worlds would be to define semantically grounded vector representation (feature embedding) of logic formulae, thus enabling to perform continuous learning and optimization in the semantic space of formulae. We tackle this goal for knowledge expressed in Signal Temporal Logic (STL) and devise a method to compute continuous embeddings of formulae with several desirable properties: the embedding (i) is finite-dimensional, (ii) faithfully reflects the semantics of the formulae, (iii) does not require any learning but instead is defined from basic principles, (iv) is interpretable. Another significant contribution lies in demonstrating the efficacy of the approach in two tasks: learning model checking, where we predict the probability of requirements being satisfied in stochastic processes; and integrating the embeddings into a neuro-symbolic framework, to constrain the output of a deep-learning generative model to comply to a given logical specification.

ECATS: Explainable-by-design concept-based anomaly detection for time series

Deep learning methods for time series have already reached excellent performances in both prediction and classification tasks, including anomaly detection. However, the complexity inherent in Cyber Physical Systems (CPS) creates a challenge when it comes to explainability methods. To overcome this inherent lack of interpretability, we propose ECATS, a concept-based neuro-symbolic architecture where concepts are represented as Signal Temporal Logic (STL) formulae. Leveraging kernel-based methods for STL, concept embeddings are learnt in an unsupervised manner through a cross-attention mechanism. The network makes class predictions through these concept embeddings, allowing for a meaningful explanation to be naturally extracted for each input. Our preliminary experiments with a simple CPS-based dataset show that our model is able to achieve great classification performance while ensuring local interpretability.

Learning Model Checking and the Kernel Trick for Signal Temporal Logic on Stochastic Processes

We introduce a similarity function on formulae of signal temporal logic (STL). It comes in the form of a kernel function, well known in machine learning as a conceptually and computationally efficient tool. The corresponding kernel trick allows us to circumvent the complicated process of feature extraction, i.e. the (typically manual) effort to identify the decisive properties of formulae so that learning can be applied. We demonstrate this consequence and its advantages on the task of predicting (quantitative) satisfaction of STL formulae on stochastic processes: Using our kernel and the kernel trick, we learn (i) computationally efficiently (ii) a practically precise predictor of satisfaction, (iii) avoiding the difficult task of finding a way to explicitly turn formulae into vectors of numbers in a sensible way. We back the high precision we have achieved in the experiments by a theoretically sound PAC guarantee, ensuring our procedure efficiently delivers a close-to-optimal predictor.

Mining Interpretable Spatio-temporal Logic Properties for Spatially Distributed Systems

The Internet-of-Things, complex sensor networks, multi-agent cyber-physical systems are all examples of spatially distributed systems that continuously evolve in time. Such systems generate huge amounts of spatio-temporal data, and system designers are often interested in analyzing and discovering structure within the data. There has been considerable interest in learning causal and logical properties of temporal data using logics such as Signal Temporal Logic (STL); however, there is limited work on discovering such relations on spatio-temporal data. We propose the first set of algorithms for unsupervised learning for spatio-temporal data. Our method does automatic feature extraction from the spatio-temporal data by projecting it onto the parameter space of a parametric spatio-temporal reach and escape logic (PSTREL). We propose an agglomerative hierarchical clustering technique that guarantees that each cluster satisfies a distinct STREL formula. We show that our method generates STREL formulas of bounded description complexity using a novel decision-tree approach which generalizes previous unsupervised learning techniques for Signal Temporal Logic. We demonstrate the effectiveness of our approach on case studies from diverse domains such as urban transportation, epidemiology, green infrastructure, and air quality monitoring.

A kernel function for Signal Temporal Logic formulae

We discuss how to define a kernel for Signal Temporal Logic (STL) formulae. Such a kernel allows us to embed the space of formulae into a Hilbert space, and opens up the use of kernel-based machine learning algorithms in the context of STL. We show an application of this idea to a regression problem in formula space for probabilistic models.

A Robust Genetic Algorithm for Learning Temporal Specifications from Data

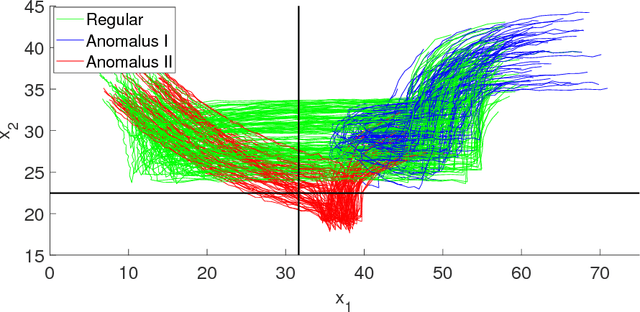
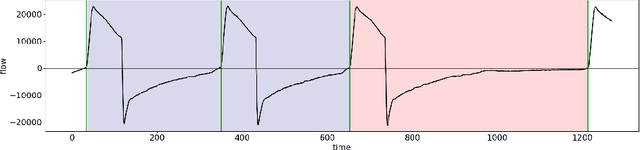
We consider the problem of mining signal temporal logical requirements from a dataset of regular (good) and anomalous (bad) trajectories of a dynamical system. We assume the training set to be labeled by human experts and that we have access only to a limited amount of data, typically noisy. We provide a systematic approach to synthesize both the syntactical structure and the parameters of the temporal logic formula using a two-steps procedure: first, we leverage a novel evolutionary algorithm for learning the structure of the formula; second, we perform the parameter synthesis operating on the statistical emulation of the average robustness for a candidate formula w.r.t. its parameters. We compare our results with our previous work [{BufoBSBLB14] and with a recently proposed decision-tree [bombara_decision_2016] based method. We present experimental results on two case studies: an anomalous trajectory detection problem of a naval surveillance system and the characterization of an Ineffective Respiratory effort, showing the usefulness of our work.

On the Robustness of Temporal Properties for Stochastic Models

Stochastic models such as Continuous-Time Markov Chains (CTMC) and Stochastic Hybrid Automata (SHA) are powerful formalisms to model and to reason about the dynamics of biological systems, due to their ability to capture the stochasticity inherent in biological processes. A classical question in formal modelling with clear relevance to biological modelling is the model checking problem. i.e. calculate the probability that a behaviour, expressed for instance in terms of a certain temporal logic formula, may occur in a given stochastic process. However, one may not only be interested in the notion of satisfiability, but also in the capacity of a system to mantain a particular emergent behaviour unaffected by the perturbations, caused e.g. from extrinsic noise, or by possible small changes in the model parameters. To address this issue, researchers from the verification community have recently proposed several notions of robustness for temporal logic providing suitable definitions of distance between a trajectory of a (deterministic) dynamical system and the boundaries of the set of trajectories satisfying the property of interest. The contributions of this paper are twofold. First, we extend the notion of robustness to stochastic systems, showing that this naturally leads to a distribution of robustness scores. By discussing two examples, we show how to approximate the distribution of the robustness score and its key indicators: the average robustness and the conditional average robustness. Secondly, we show how to combine these indicators with the satisfaction probability to address the system design problem, where the goal is to optimize some control parameters of a stochastic model in order to best maximize robustness of the desired specifications.