Differentiable Forward Projector for X-ray Computed Tomography

Data-driven deep learning has been successfully applied to various computed tomographic reconstruction problems. The deep inference models may outperform existing analytical and iterative algorithms, especially in ill-posed CT reconstruction. However, those methods often predict images that do not agree with the measured projection data. This paper presents an accurate differentiable forward and back projection software library to ensure the consistency between the predicted images and the original measurements. The software library efficiently supports various projection geometry types while minimizing the GPU memory footprint requirement, which facilitates seamless integration with existing deep learning training and inference pipelines. The proposed software is available as open source: https://github.com/LLNL/LEAP.

Dynamic CT Reconstruction from Limited Views with Implicit Neural Representations and Parametric Motion Fields

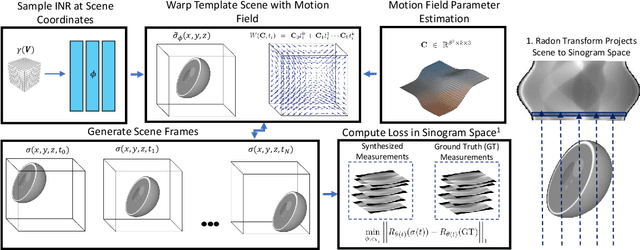
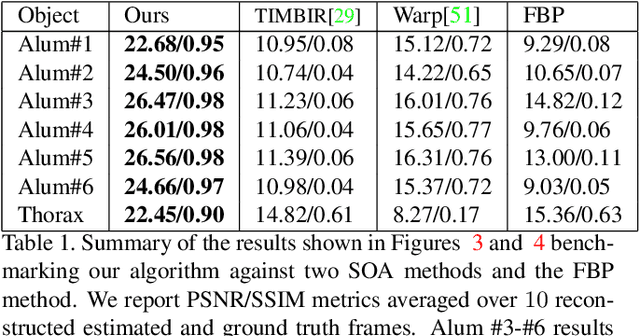
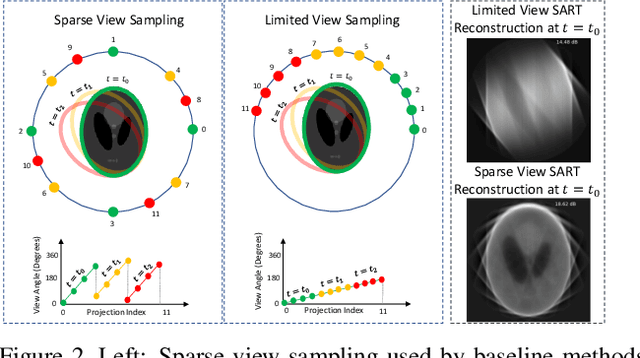
Reconstructing dynamic, time-varying scenes with computed tomography (4D-CT) is a challenging and ill-posed problem common to industrial and medical settings. Existing 4D-CT reconstructions are designed for sparse sampling schemes that require fast CT scanners to capture multiple, rapid revolutions around the scene in order to generate high quality results. However, if the scene is moving too fast, then the sampling occurs along a limited view and is difficult to reconstruct due to spatiotemporal ambiguities. In this work, we design a reconstruction pipeline using implicit neural representations coupled with a novel parametric motion field warping to perform limited view 4D-CT reconstruction of rapidly deforming scenes. Importantly, we utilize a differentiable analysis-by-synthesis approach to compare with captured x-ray sinogram data in a self-supervised fashion. Thus, our resulting optimization method requires no training data to reconstruct the scene. We demonstrate that our proposed system robustly reconstructs scenes containing deformable and periodic motion and validate against state-of-the-art baselines. Further, we demonstrate an ability to reconstruct continuous spatiotemporal representations of our scenes and upsample them to arbitrary volumes and frame rates post-optimization. This research opens a new avenue for implicit neural representations in computed tomography reconstruction in general.

Extreme Few-view CT Reconstruction using Deep Inference

Reconstruction of few-view x-ray Computed Tomography (CT) data is a highly ill-posed problem. It is often used in applications that require low radiation dose in clinical CT, rapid industrial scanning, or fixed-gantry CT. Existing analytic or iterative algorithms generally produce poorly reconstructed images, severely deteriorated by artifacts and noise, especially when the number of x-ray projections is considerably low. This paper presents a deep network-driven approach to address extreme few-view CT by incorporating convolutional neural network-based inference into state-of-the-art iterative reconstruction. The proposed method interprets few-view sinogram data using attention-based deep networks to infer the reconstructed image. The predicted image is then used as prior knowledge in the iterative algorithm for final reconstruction. We demonstrate effectiveness of the proposed approach by performing reconstruction experiments on a chest CT dataset.

Lose The Views: Limited Angle CT Reconstruction via Implicit Sinogram Completion

Computed Tomography (CT) reconstruction is a fundamental component to a wide variety of applications ranging from security, to healthcare. The classical techniques require measuring projections, called sinograms, from a full 180$^\circ$ view of the object. This is impractical in a limited angle scenario, when the viewing angle is less than 180$^\circ$, which can occur due to different factors including restrictions on scanning time, limited flexibility of scanner rotation, etc. The sinograms obtained as a result, cause existing techniques to produce highly artifact-laden reconstructions. In this paper, we propose to address this problem through implicit sinogram completion, on a challenging real world dataset containing scans of common checked-in luggage. We propose a system, consisting of 1D and 2D convolutional neural networks, that operates on a limited angle sinogram to directly produce the best estimate of a reconstruction. Next, we use the x-ray transform on this reconstruction to obtain a "completed" sinogram, as if it came from a full 180$^\circ$ measurement. We feed this to standard analytical and iterative reconstruction techniques to obtain the final reconstruction. We show with extensive experimentation that this combined strategy outperforms many competitive baselines. We also propose a measure of confidence for the reconstruction that enables a practitioner to gauge the reliability of a prediction made by our network. We show that this measure is a strong indicator of quality as measured by the PSNR, while not requiring ground truth at test time. Finally, using a segmentation experiment, we show that our reconstruction preserves the 3D structure of objects effectively.