Kyle Akira Rocha
Emulators for stellar profiles in binary population modeling
Oct 14, 2024



Abstract:Knowledge about the internal physical structure of stars is crucial to understanding their evolution. The novel binary population synthesis code POSYDON includes a module for interpolating the stellar and binary properties of any system at the end of binary MESA evolution based on a pre-computed set of models. In this work, we present a new emulation method for predicting stellar profiles, i.e., the internal stellar structure along the radial axis, using machine learning techniques. We use principal component analysis for dimensionality reduction and fully-connected feed-forward neural networks for making predictions. We find accuracy to be comparable to that of nearest neighbor approximation, with a strong advantage in terms of memory and storage efficiency. By delivering more information about the evolution of stellar internal structure, these emulators will enable faster simulations of higher physical fidelity with large-scale simulations of binary star population synthesis possible with POSYDON and other population synthesis codes.
Active Learning for Computationally Efficient Distribution of Binary Evolution Simulations
Mar 30, 2022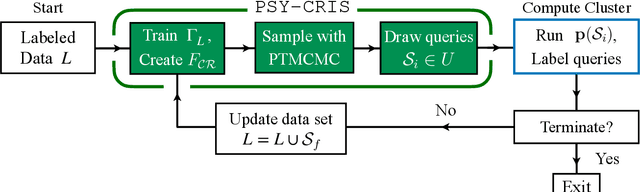

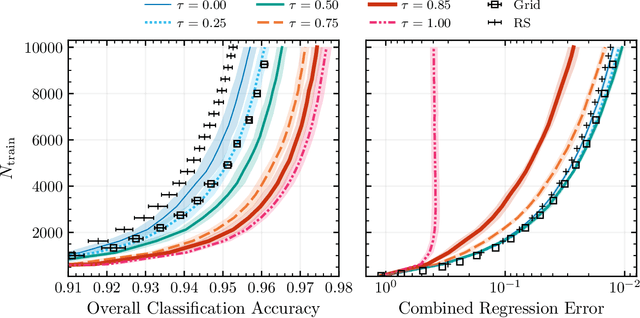
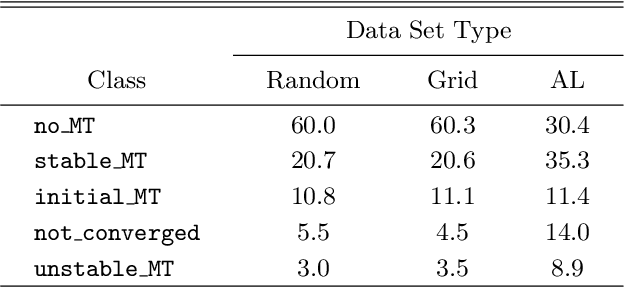
Abstract:Binary stars undergo a variety of interactions and evolutionary phases, critical for predicting and explaining observed properties. Binary population synthesis with full stellar-structure and evolution simulations are computationally expensive requiring a large number of mass-transfer sequences. The recently developed binary population synthesis code POSYDON incorporates grids of MESA binary star simulations which are then interpolated to model large-scale populations of massive binaries. The traditional method of computing a high-density rectilinear grid of simulations is not scalable for higher-dimension grids, accounting for a range of metallicities, rotation, and eccentricity. We present a new active learning algorithm, psy-cris, which uses machine learning in the data-gathering process to adaptively and iteratively select targeted simulations to run, resulting in a custom, high-performance training set. We test psy-cris on a toy problem and find the resulting training sets require fewer simulations for accurate classification and regression than either regular or randomly sampled grids. We further apply psy-cris to the target problem of building a dynamic grid of MESA simulations, and we demonstrate that, even without fine tuning, a simulation set of only $\sim 1/4$ the size of a rectilinear grid is sufficient to achieve the same classification accuracy. We anticipate further gains when algorithmic parameters are optimized for the targeted application. We find that optimizing for classification only may lead to performance losses in regression, and vice versa. Lowering the computational cost of producing grids will enable future versions of POSYDON to cover more input parameters while preserving interpolation accuracies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge