Statistical Mechanics of Strahler Number via Random and Natural Language Sentences

The Strahler number was originally proposed to characterize the complexity of river bifurcation and has found various applications. This article proposes computation of the Strahler number's upper and lower limits for natural language sentence tree structures, which are available in a large dataset allowing for statistical mechanics analysis. Through empirical measurements across grammatically annotated data, the Strahler number of natural language sentences is shown to be almost always 3 or 4, similar to the case of river bifurcation as reported by Strahler (1957) and Horton (1945). From the theory behind the number, we show that it is the lower limit of the amount of memory required to process sentences under a particular model. A mathematical analysis of random trees provides a further conjecture on the nature of the Strahler number, revealing that it is not a constant but grows logarithmically. This finding uncovers the statistical basics behind the Strahler number as a characteristic of a general tree structure target.

A Comparison of Two Fluctuation Analyses for Natural Language Clustering Phenomena: Taylor and Ebeling & Neiman Methods

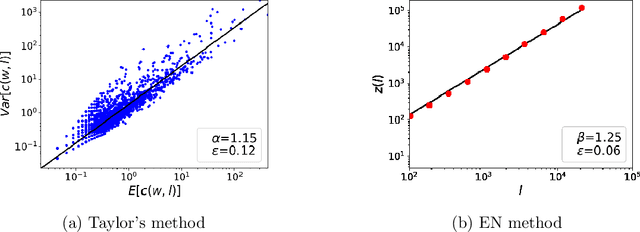
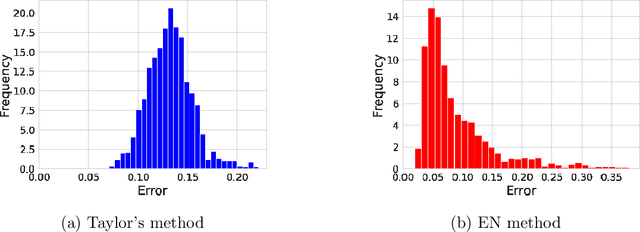
This article considers the fluctuation analysis methods of Taylor and Ebeling & Neiman. While both have been applied to various phenomena in the statistical mechanics domain, their similarities and differences have not been clarified. After considering their analytical aspects, this article presents a large-scale application of these methods to text. It is found that both methods can distinguish real text from independently and identically distributed (i.i.d.) sequences. Furthermore, it is found that the Taylor exponents acquired from words can roughly distinguish text categories; this is also the case for Ebeling and Neiman exponents, but to a lesser extent. Additionally, both methods show some possibility of capturing script kinds.

Extraction of Templates from Phrases Using Sequence Binary Decision Diagrams

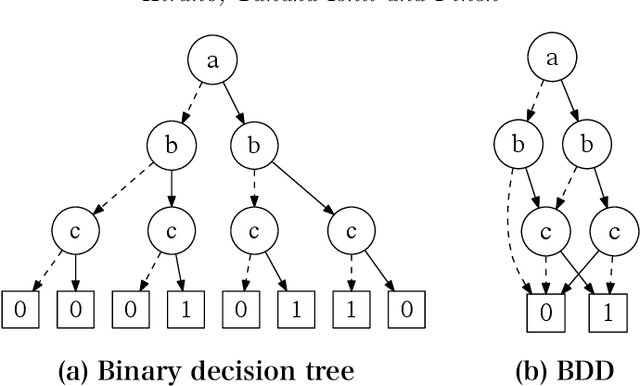
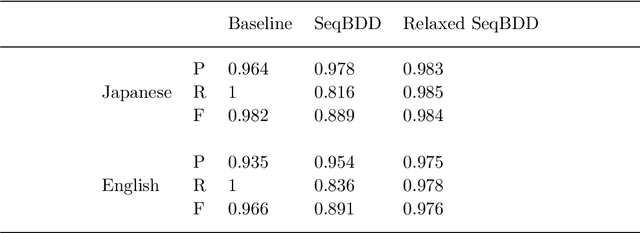
The extraction of templates such as ``regard X as Y'' from a set of related phrases requires the identification of their internal structures. This paper presents an unsupervised approach for extracting templates on-the-fly from only tagged text by using a novel relaxed variant of the Sequence Binary Decision Diagram (SeqBDD). A SeqBDD can compress a set of sequences into a graphical structure equivalent to a minimal DFA, but more compact and better suited to the task of template extraction. The main contribution of this paper is a relaxed form of the SeqBDD construction algorithm that enables it to form general representations from a small amount of data. The process of compression of shared structures in the text during Relaxed SeqBDD construction, naturally induces the templates we wish to extract. Experiments show that the method is capable of high-quality extraction on tasks based on verb+preposition templates from corpora and phrasal templates from short messages from social media.

Evaluating Computational Language Models with Scaling Properties of Natural Language

In this article, we evaluate computational models of natural language with respect to the universal statistical behaviors of natural language. Statistical mechanical analyses have revealed that natural language text is characterized by scaling properties, which quantify the global structure in the vocabulary population and the long memory of a text. We study whether five scaling properties (given by Zipf's law, Heaps' law, Ebeling's method, Taylor's law, and long-range correlation analysis) can serve for evaluation of computational models. Specifically, we test $n$-gram language models, a probabilistic context-free grammar (PCFG), language models based on Simon/Pitman-Yor processes, neural language models, and generative adversarial networks (GANs) for text generation. Our analysis reveals that language models based on recurrent neural networks (RNNs) with a gating mechanism (i.e., long short-term memory, LSTM; a gated recurrent unit, GRU; and quasi-recurrent neural networks, QRNNs) are the only computational models that can reproduce the long memory behavior of natural language. Furthermore, through comparison with recently proposed model-based evaluation methods, we find that the exponent of Taylor's law is a good indicator of model quality.

Word Familiarity and Frequency

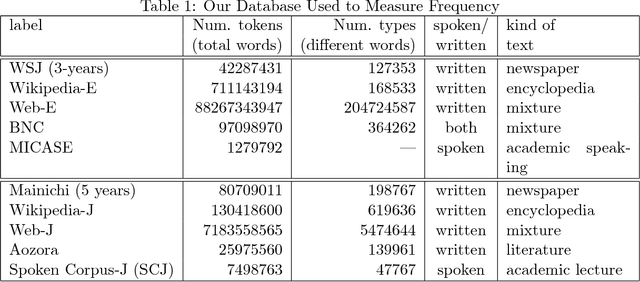
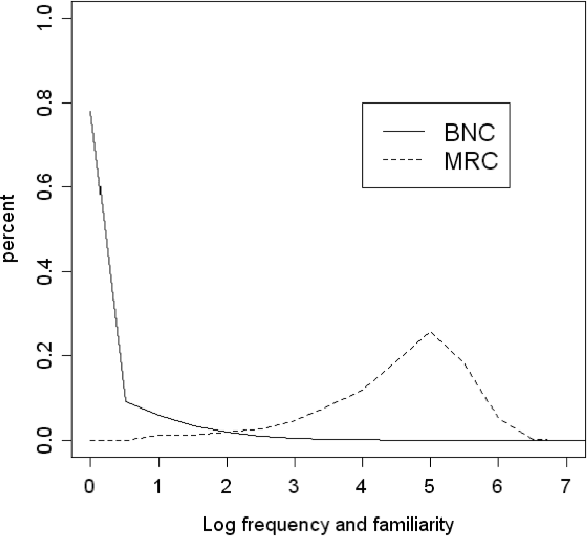
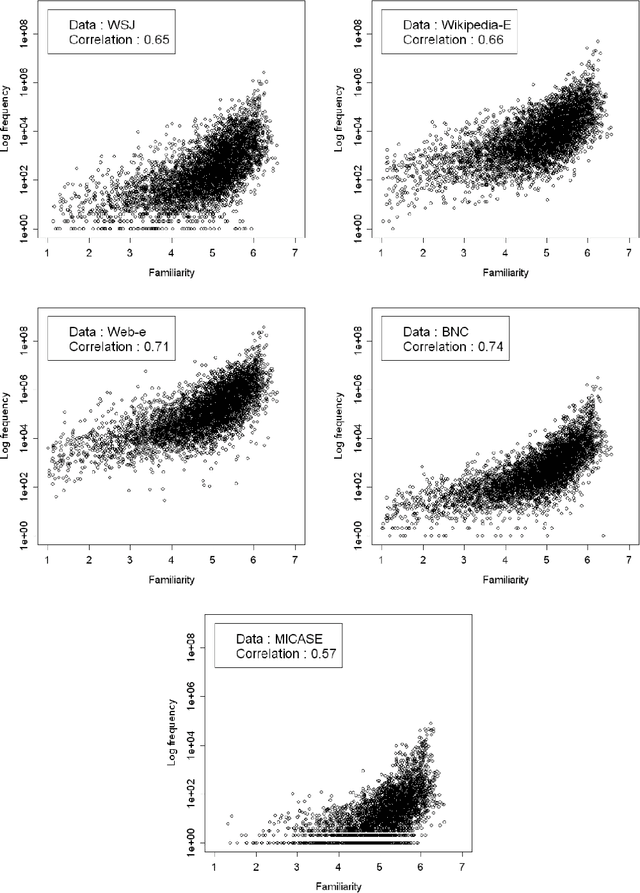
Word frequency is assumed to correlate with word familiarity, but the strength of this correlation has not been thoroughly investigated. In this paper, we report on our analysis of the correlation between a word familiarity rating list obtained through a psycholinguistic experiment and the log-frequency obtained from various corpora of different kinds and sizes (up to the terabyte scale) for English and Japanese. Major findings are threefold: First, for a given corpus, familiarity is necessary for a word to achieve high frequency, but familiar words are not necessarily frequent. Second, correlation increases with the corpus data size. Third, a corpus of spoken language correlates better than one of written language. These findings suggest that cognitive familiarity ratings are correlated to frequency, but more highly to that of spoken rather than written language.

Taylor's law for Human Linguistic Sequences

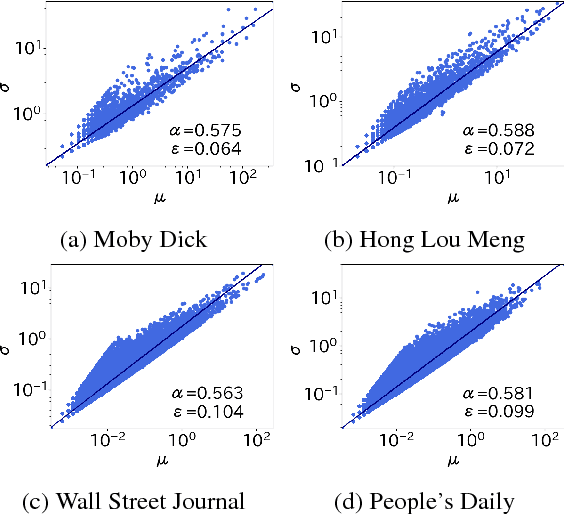
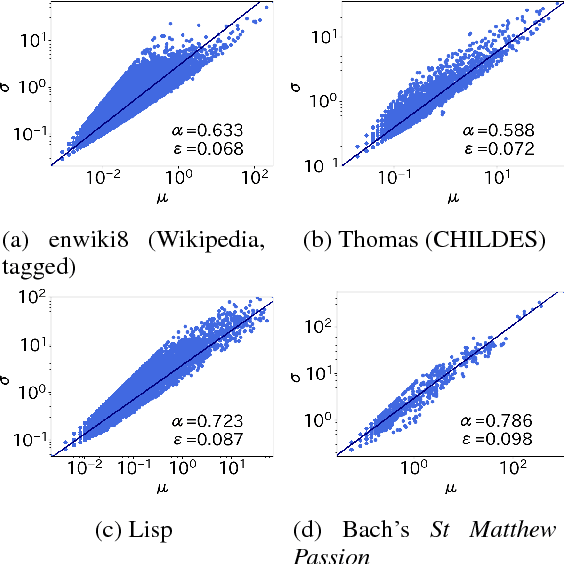
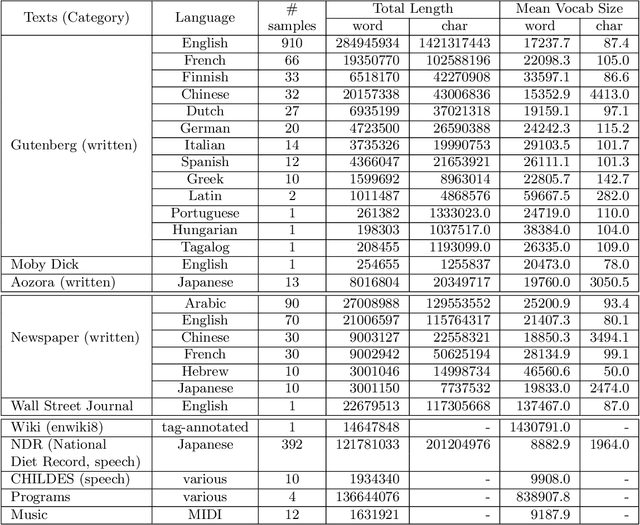
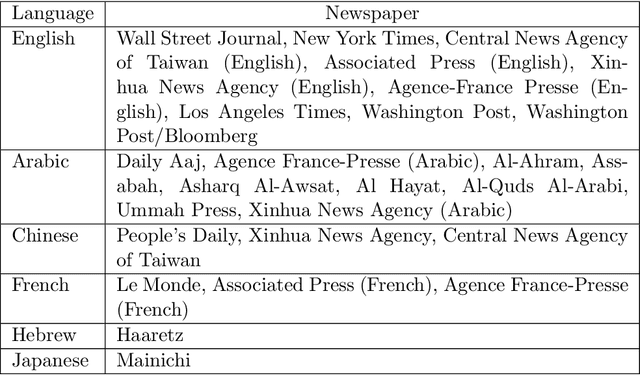
Taylor's law describes the fluctuation characteristics underlying a system in which the variance of an event within a time span grows by a power law with respect to the mean. Although Taylor's law has been applied in many natural and social systems, its application for language has been scarce. This article describes a new quantification of Taylor's law in natural language and reports an analysis of over 1100 texts across 14 languages. The Taylor exponents of written natural language texts were found to exhibit almost the same value. The exponent was also compared for other language-related data, such as the child-directed speech, music, and programming language code. The results show how the Taylor exponent serves to quantify the fundamental structural complexity underlying linguistic time series. The article also shows the applicability of these findings in evaluating language models.

Assessing Language Models with Scaling Properties

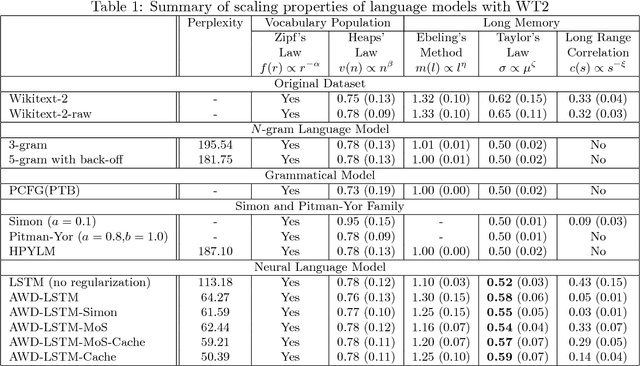
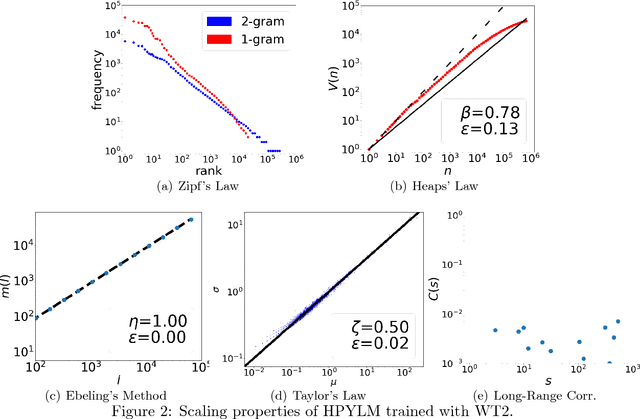
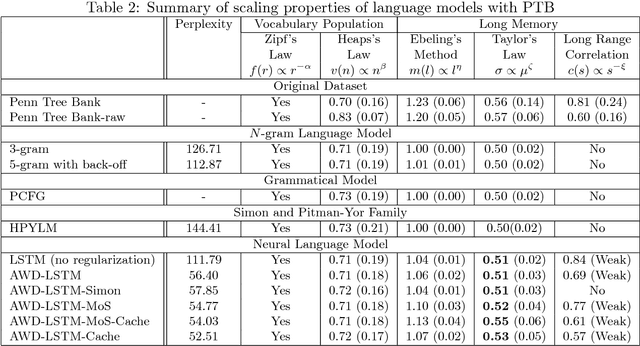
Language models have primarily been evaluated with perplexity. While perplexity quantifies the most comprehensible prediction performance, it does not provide qualitative information on the success or failure of models. Another approach for evaluating language models is thus proposed, using the scaling properties of natural language. Five such tests are considered, with the first two accounting for the vocabulary population and the other three for the long memory of natural language. The following models were evaluated with these tests: n-grams, probabilistic context-free grammar (PCFG), Simon and Pitman-Yor (PY) processes, hierarchical PY, and neural language models. Only the neural language models exhibit the long memory properties of natural language, but to a limited degree. The effectiveness of every test of these models is also discussed.

Long-Range Correlation Underlying Childhood Language and Generative Models

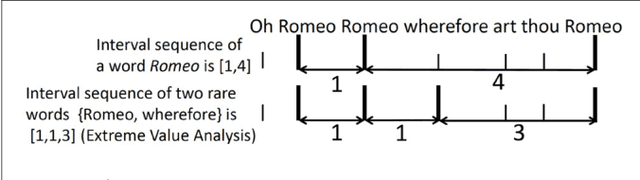
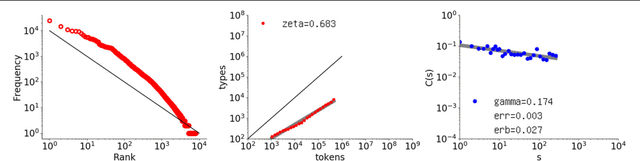
Long-range correlation, a property of time series exhibiting long-term memory, is mainly studied in the statistical physics domain and has been reported to exist in natural language. Using a state-of-the-art method for such analysis, long-range correlation is first shown to occur in long CHILDES data sets. To understand why, Bayesian generative models of language, originally proposed in the cognitive scientific domain, are investigated. Among representative models, the Simon model was found to exhibit surprisingly good long-range correlation, but not the Pitman-Yor model. Since the Simon model is known not to correctly reflect the vocabulary growth of natural language, a simple new model is devised as a conjunct of the Simon and Pitman-Yor models, such that long-range correlation holds with a correct vocabulary growth rate. The investigation overall suggests that uniform sampling is one cause of long-range correlation and could thus have a relation with actual linguistic processes.

Do Neural Nets Learn Statistical Laws behind Natural Language?

The performance of deep learning in natural language processing has been spectacular, but the reasons for this success remain unclear because of the inherent complexity of deep learning. This paper provides empirical evidence of its effectiveness and of a limitation of neural networks for language engineering. Precisely, we demonstrate that a neural language model based on long short-term memory (LSTM) effectively reproduces Zipf's law and Heaps' law, two representative statistical properties underlying natural language. We discuss the quality of reproducibility and the emergence of Zipf's law and Heaps' law as training progresses. We also point out that the neural language model has a limitation in reproducing long-range correlation, another statistical property of natural language. This understanding could provide a direction for improving the architectures of neural networks.