Tatsuru Kobayashi
Taylor's law for Human Linguistic Sequences
Jun 07, 2018
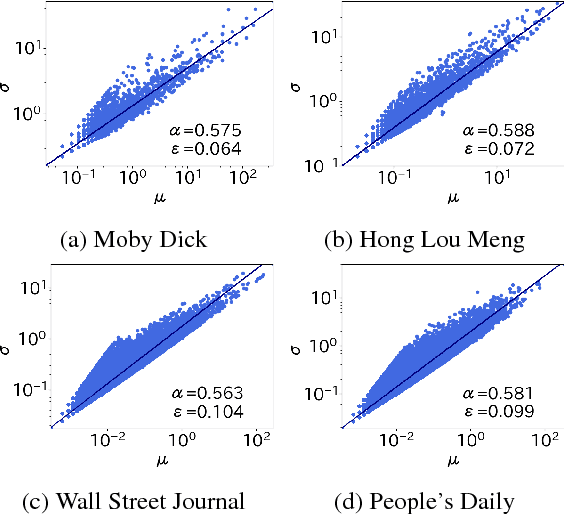

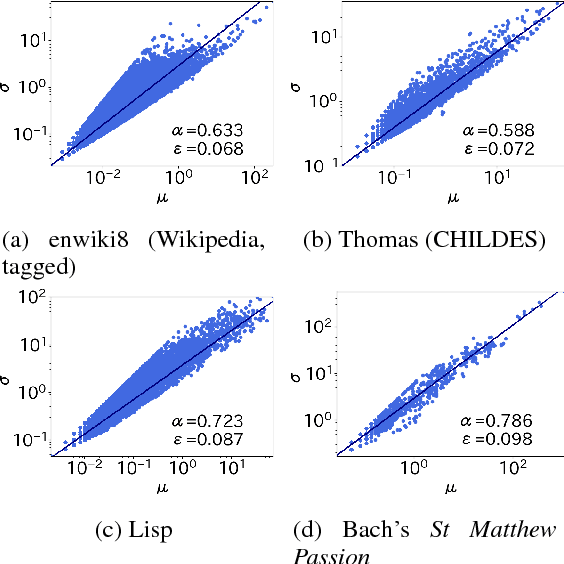
Abstract:Taylor's law describes the fluctuation characteristics underlying a system in which the variance of an event within a time span grows by a power law with respect to the mean. Although Taylor's law has been applied in many natural and social systems, its application for language has been scarce. This article describes a new quantification of Taylor's law in natural language and reports an analysis of over 1100 texts across 14 languages. The Taylor exponents of written natural language texts were found to exhibit almost the same value. The exponent was also compared for other language-related data, such as the child-directed speech, music, and programming language code. The results show how the Taylor exponent serves to quantify the fundamental structural complexity underlying linguistic time series. The article also shows the applicability of these findings in evaluating language models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge