Efficiera Residual Networks: Hardware-Friendly Fully Binary Weight with 2-bit Activation Model Achieves Practical ImageNet Accuracy

The edge-device environment imposes severe resource limitations, encompassing computation costs, hardware resource usage, and energy consumption for deploying deep neural network models. Ultra-low-bit quantization and hardware accelerators have been explored as promising approaches to address these challenges. Ultra-low-bit quantization significantly reduces the model size and the computational cost. Despite progress so far, many competitive ultra-low-bit models still partially rely on float or non-ultra-low-bit quantized computation such as the input and output layer. We introduce Efficiera Residual Networks (ERNs), a model optimized for low-resource edge devices. ERNs achieve full ultra-low-bit quantization, with all weights, including the initial and output layers, being binary, and activations set at 2 bits. We introduce the shared constant scaling factor technique to enable integer-valued computation in residual connections, allowing our model to operate without float values until the final convolution layer. Demonstrating competitiveness, ERNs achieve an ImageNet top-1 accuracy of 72.5pt with a ResNet50-compatible architecture and 63.6pt with a model size less than 1MB. Moreover, ERNs exhibit impressive inference times, reaching 300FPS with the smallest model and 60FPS with the largest model on a cost-efficient FPGA device.

A Comparison of Two Fluctuation Analyses for Natural Language Clustering Phenomena: Taylor and Ebeling & Neiman Methods

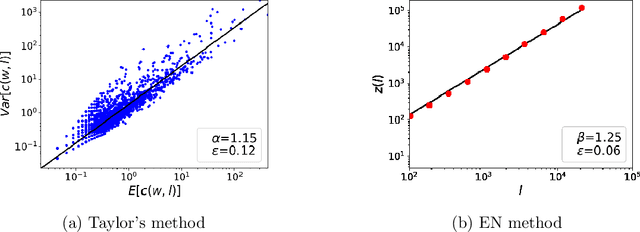
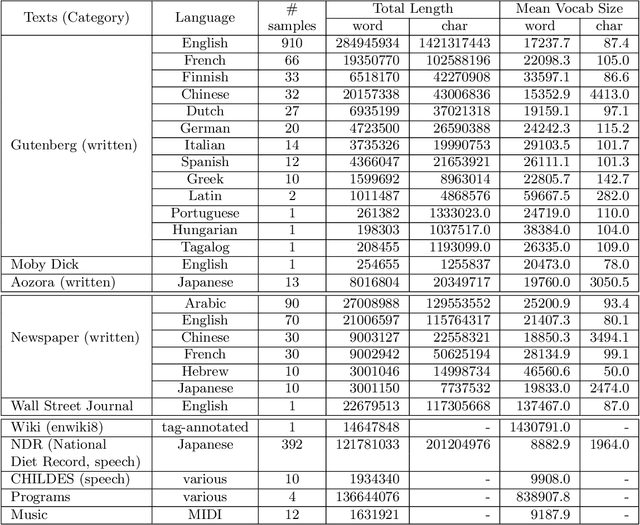
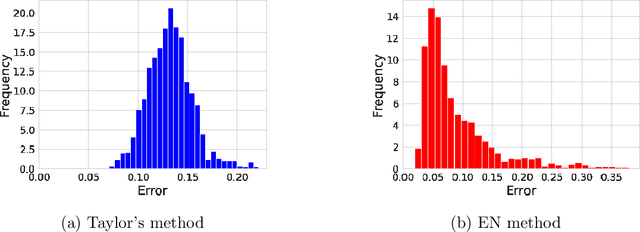
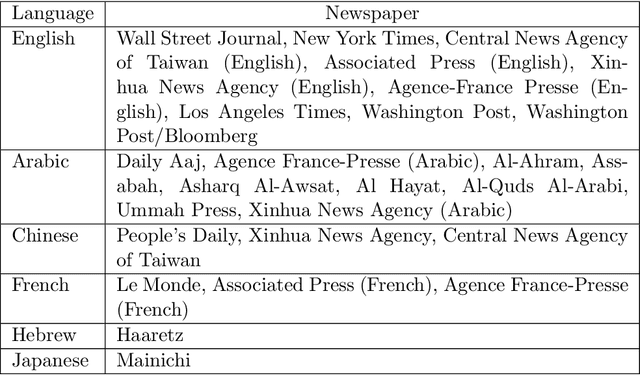
This article considers the fluctuation analysis methods of Taylor and Ebeling & Neiman. While both have been applied to various phenomena in the statistical mechanics domain, their similarities and differences have not been clarified. After considering their analytical aspects, this article presents a large-scale application of these methods to text. It is found that both methods can distinguish real text from independently and identically distributed (i.i.d.) sequences. Furthermore, it is found that the Taylor exponents acquired from words can roughly distinguish text categories; this is also the case for Ebeling and Neiman exponents, but to a lesser extent. Additionally, both methods show some possibility of capturing script kinds.

Evaluating Computational Language Models with Scaling Properties of Natural Language

In this article, we evaluate computational models of natural language with respect to the universal statistical behaviors of natural language. Statistical mechanical analyses have revealed that natural language text is characterized by scaling properties, which quantify the global structure in the vocabulary population and the long memory of a text. We study whether five scaling properties (given by Zipf's law, Heaps' law, Ebeling's method, Taylor's law, and long-range correlation analysis) can serve for evaluation of computational models. Specifically, we test $n$-gram language models, a probabilistic context-free grammar (PCFG), language models based on Simon/Pitman-Yor processes, neural language models, and generative adversarial networks (GANs) for text generation. Our analysis reveals that language models based on recurrent neural networks (RNNs) with a gating mechanism (i.e., long short-term memory, LSTM; a gated recurrent unit, GRU; and quasi-recurrent neural networks, QRNNs) are the only computational models that can reproduce the long memory behavior of natural language. Furthermore, through comparison with recently proposed model-based evaluation methods, we find that the exponent of Taylor's law is a good indicator of model quality.

Assessing Language Models with Scaling Properties

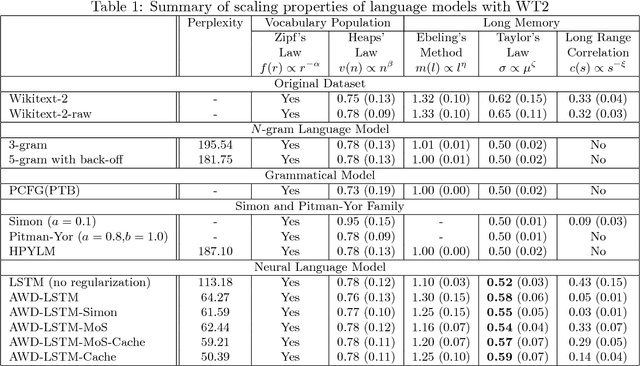
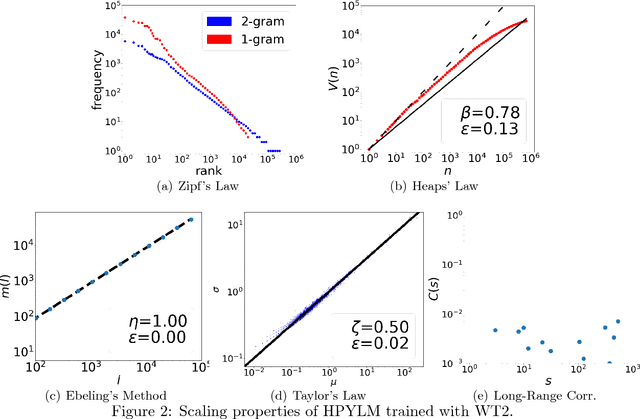
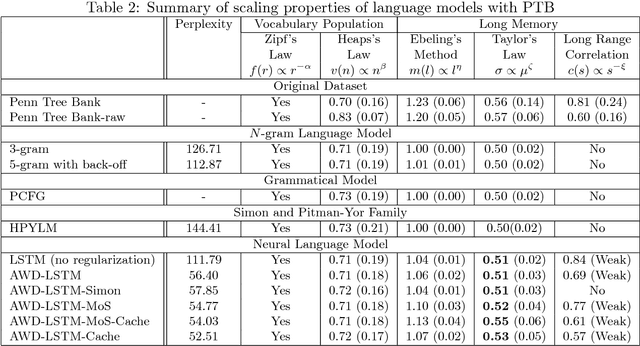
Language models have primarily been evaluated with perplexity. While perplexity quantifies the most comprehensible prediction performance, it does not provide qualitative information on the success or failure of models. Another approach for evaluating language models is thus proposed, using the scaling properties of natural language. Five such tests are considered, with the first two accounting for the vocabulary population and the other three for the long memory of natural language. The following models were evaluated with these tests: n-grams, probabilistic context-free grammar (PCFG), Simon and Pitman-Yor (PY) processes, hierarchical PY, and neural language models. Only the neural language models exhibit the long memory properties of natural language, but to a limited degree. The effectiveness of every test of these models is also discussed.

Do Neural Nets Learn Statistical Laws behind Natural Language?

The performance of deep learning in natural language processing has been spectacular, but the reasons for this success remain unclear because of the inherent complexity of deep learning. This paper provides empirical evidence of its effectiveness and of a limitation of neural networks for language engineering. Precisely, we demonstrate that a neural language model based on long short-term memory (LSTM) effectively reproduces Zipf's law and Heaps' law, two representative statistical properties underlying natural language. We discuss the quality of reproducibility and the emergence of Zipf's law and Heaps' law as training progresses. We also point out that the neural language model has a limitation in reproducing long-range correlation, another statistical property of natural language. This understanding could provide a direction for improving the architectures of neural networks.