Online Incident Response Planning under Model Misspecification through Bayesian Learning and Belief Quantization

Effective responses to cyberattacks require fast decisions, even when information about the attack is incomplete or inaccurate. However, most decision-support frameworks for incident response rely on a detailed system model that describes the incident, which restricts their practical utility. In this paper, we address this limitation and present an online method for incident response planning under model misspecification, which we call MOBAL: Misspecified Online Bayesian Learning. MOBAL iteratively refines a conjecture about the model through Bayesian learning as new information becomes available, which facilitates model adaptation as the incident unfolds. To determine effective responses online, we quantize the conjectured model into a finite Markov model, which enables efficient response planning through dynamic programming. We prove that Bayesian learning is asymptotically consistent with respect to the information feedback. Additionally, we establish bounds on misspecification and quantization errors. Experiments on the CAGE-2 benchmark show that MOBAL outperforms the state of the art in terms of adaptability and robustness to model misspecification.

Incident Response Planning Using a Lightweight Large Language Model with Reduced Hallucination

Timely and effective incident response is key to managing the growing frequency of cyberattacks. However, identifying the right response actions for complex systems is a major technical challenge. A promising approach to mitigate this challenge is to use the security knowledge embedded in large language models (LLMs) to assist security operators during incident handling. Recent research has demonstrated the potential of this approach, but current methods are mainly based on prompt engineering of frontier LLMs, which is costly and prone to hallucinations. We address these limitations by presenting a novel way to use an LLM for incident response planning with reduced hallucination. Our method includes three steps: fine-tuning, information retrieval, and lookahead planning. We prove that our method generates response plans with a bounded probability of hallucination and that this probability can be made arbitrarily small at the expense of increased planning time under certain assumptions. Moreover, we show that our method is lightweight and can run on commodity hardware. We evaluate our method on logs from incidents reported in the literature. The experimental results show that our method a) achieves up to 22% shorter recovery times than frontier LLMs and b) generalizes to a broad range of incident types and response actions.

Optimal Defender Strategies for CAGE-2 using Causal Modeling and Tree Search

The CAGE-2 challenge is considered a standard benchmark to compare methods for autonomous cyber defense. Current state-of-the-art methods evaluated against this benchmark are based on model-free (offline) reinforcement learning, which does not provide provably optimal defender strategies. We address this limitation and present a formal (causal) model of CAGE-2 together with a method that produces a provably optimal defender strategy, which we call Causal Partially Observable Monte-Carlo Planning (C-POMCP). It has two key properties. First, it incorporates the causal structure of the target system, i.e., the causal relationships among the system variables. This structure allows for a significant reduction of the search space of defender strategies. Second, it is an online method that updates the defender strategy at each time step via tree search. Evaluations against the CAGE-2 benchmark show that C-POMCP achieves state-of-the-art performance with respect to effectiveness and is two orders of magnitude more efficient in computing time than the closest competitor method.

Intrusion Tolerance for Networked Systems through Two-Level Feedback Control

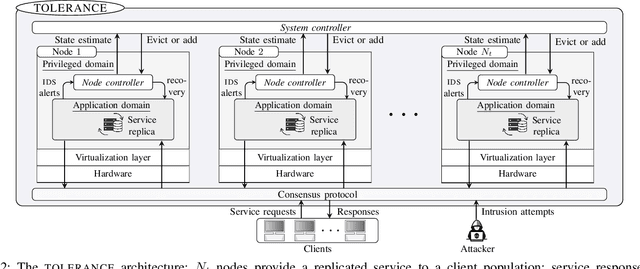
We formulate intrusion tolerance for a system with service replicas as a two-level optimal control problem. On the local level node controllers perform intrusion recovery, and on the global level a system controller manages the replication factor. The local and global control problems can be formulated as classical problems in operations research, namely, the machine replacement problem and the inventory replenishment problem. Based on this formulation, we design TOLERANCE, a novel control architecture for intrusion-tolerant systems. We prove that the optimal control strategies on both levels have threshold structure and design efficient algorithms for computing them. We implement and evaluate TOLERANCE in an emulation environment where we run 10 types of network intrusions. The results show that TOLERANCE can improve service availability and reduce operational cost compared with state-of-the-art intrusion-tolerant systems.

Conjectural Online Learning with First-order Beliefs in Asymmetric Information Stochastic Games

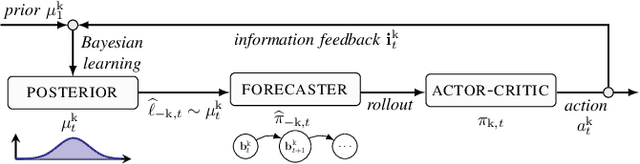
Asymmetric information stochastic games (\textsc{aisg}s) arise in many complex socio-technical systems, such as cyber-physical systems and IT infrastructures. Existing computational methods for \textsc{aisg}s are primarily offline and can not adapt to equilibrium deviations. Further, current methods are limited to special classes of \textsc{aisg}s to avoid belief hierarchies. To address these limitations, we propose conjectural online learning (\textsc{col}), an online method for generic \textsc{aisg}s. \textsc{col} uses a forecaster-actor-critic (\textsc{fac}) architecture where subjective forecasts are used to conjecture the opponents' strategies within a lookahead horizon, and Bayesian learning is used to calibrate the conjectures. To adapt strategies to nonstationary environments, \textsc{col} uses online rollout with cost function approximation (actor-critic). We prove that the conjectures produced by \textsc{col} are asymptotically consistent with the information feedback in the sense of a relaxed Bayesian consistency. We also prove that the empirical strategy profile induced by \textsc{col} converges to the Berk-Nash equilibrium, a solution concept characterizing rationality under subjectivity. Experimental results from an intrusion response use case demonstrate \textsc{col}'s superiority over state-of-the-art reinforcement learning methods against nonstationary attacks.

Automated Security Response through Online Learning with Adaptive Conjectures

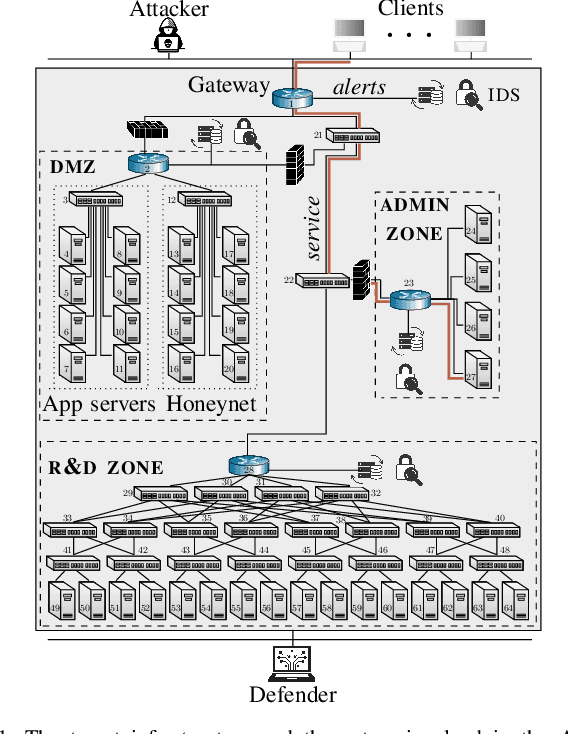
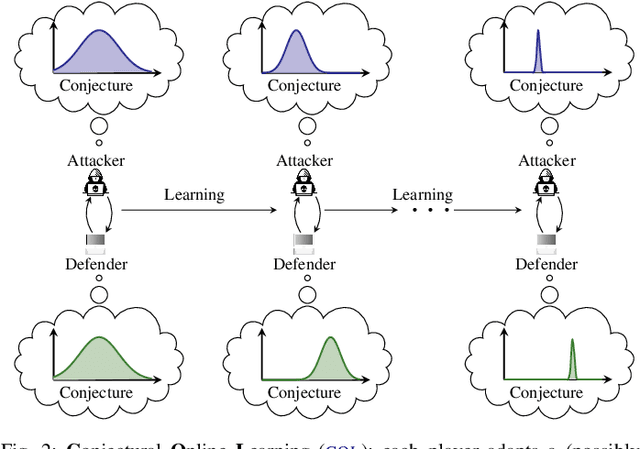
We study automated security response for an IT infrastructure and formulate the interaction between an attacker and a defender as a partially observed, non-stationary game. We relax the standard assumption that the game model is correctly specified and consider that each player has a probabilistic conjecture about the model, which may be misspecified in the sense that the true model has probability 0. This formulation allows us to capture uncertainty about the infrastructure and the intents of the players. To learn effective game strategies online, we design a novel method where a player iteratively adapts its conjecture using Bayesian learning and updates its strategy through rollout. We prove that the conjectures converge to best fits, and we provide a bound on the performance improvement that rollout enables with a conjectured model. To characterize the steady state of the game, we propose a variant of the Berk-Nash equilibrium. We present our method through an advanced persistent threat use case. Simulation studies based on testbed measurements show that our method produces effective security strategies that adapt to a changing environment. We also find that our method enables faster convergence than current reinforcement learning techniques.

Scalable Learning of Intrusion Responses through Recursive Decomposition

We study automated intrusion response for an IT infrastructure and formulate the interaction between an attacker and a defender as a partially observed stochastic game. To solve the game we follow an approach where attack and defense strategies co-evolve through reinforcement learning and self-play toward an equilibrium. Solutions proposed in previous work prove the feasibility of this approach for small infrastructures but do not scale to realistic scenarios due to the exponential growth in computational complexity with the infrastructure size. We address this problem by introducing a method that recursively decomposes the game into subgames which can be solved in parallel. Applying optimal stopping theory we show that the best response strategies in these subgames exhibit threshold structures, which allows us to compute them efficiently. To solve the decomposed game we introduce an algorithm called Decompositional Fictitious Self-Play (DFSP), which learns Nash equilibria through stochastic approximation. We evaluate the learned strategies in an emulation environment where real intrusions and response actions can be executed. The results show that the learned strategies approximate an equilibrium and that DFSP significantly outperforms a state-of-the-art algorithm for a realistic infrastructure configuration.

Optimal Observation-Intervention Trade-Off in Optimisation Problems with Causal Structure

We consider the problem of optimising an expensive-to-evaluate grey-box objective function, within a finite budget, where known side-information exists in the form of the causal structure between the design variables. Standard black-box optimisation ignores the causal structure, often making it inefficient and expensive. The few existing methods that consider the causal structure are myopic and do not fully accommodate the observation-intervention trade-off that emerges when estimating causal effects. In this paper, we show that the observation-intervention trade-off can be formulated as a non-myopic optimal stopping problem which permits an efficient solution. We give theoretical results detailing the structure of the optimal stopping times and demonstrate the generality of our approach by showing that it can be integrated with existing causal Bayesian optimisation algorithms. Experimental results show that our formulation can enhance existing algorithms on real and synthetic benchmarks.

Learning Near-Optimal Intrusion Responses Against Dynamic Attackers

We study automated intrusion response and formulate the interaction between an attacker and a defender as an optimal stopping game where attack and defense strategies evolve through reinforcement learning and self-play. The game-theoretic modeling enables us to find defender strategies that are effective against a dynamic attacker, i.e. an attacker that adapts its strategy in response to the defender strategy. Further, the optimal stopping formulation allows us to prove that optimal strategies have threshold properties. To obtain near-optimal defender strategies, we develop Threshold Fictitious Self-Play (T-FP), a fictitious self-play algorithm that learns Nash equilibria through stochastic approximation. We show that T-FP outperforms a state-of-the-art algorithm for our use case. The experimental part of this investigation includes two systems: a simulation system where defender strategies are incrementally learned and an emulation system where statistics are collected that drive simulation runs and where learned strategies are evaluated. We argue that this approach can produce effective defender strategies for a practical IT infrastructure.

Learning Security Strategies through Game Play and Optimal Stopping

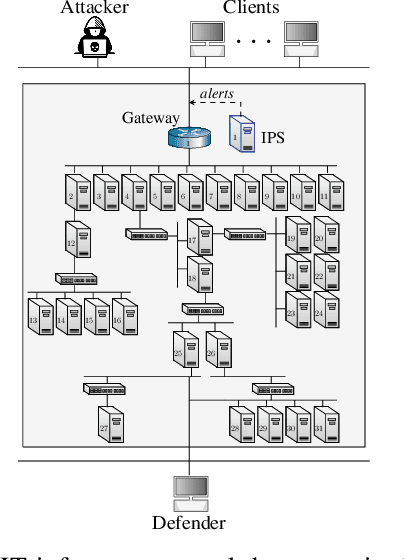
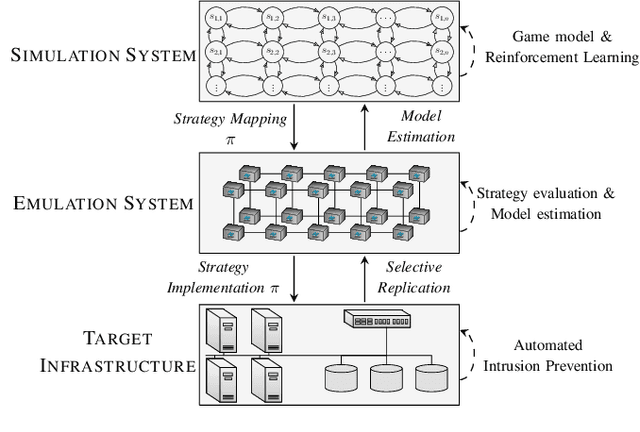
We study automated intrusion prevention using reinforcement learning. Following a novel approach, we formulate the interaction between an attacker and a defender as an optimal stopping game and let attack and defense strategies evolve through reinforcement learning and self-play. The game-theoretic perspective allows us to find defender strategies that are effective against dynamic attackers. The optimal stopping formulation gives us insight into the structure of optimal strategies, which we show to have threshold properties. To obtain the optimal defender strategies, we introduce T-FP, a fictitious self-play algorithm that learns Nash equilibria through stochastic approximation. We show that T-FP outperforms a state-of-the-art algorithm for our use case. Our overall method for learning and evaluating strategies includes two systems: a simulation system where defender strategies are incrementally learned and an emulation system where statistics are produced that drive simulation runs and where learned strategies are evaluated. We conclude that this approach can produce effective defender strategies for a practical IT infrastructure.