Automated Security Response through Online Learning with Adaptive Conjectures

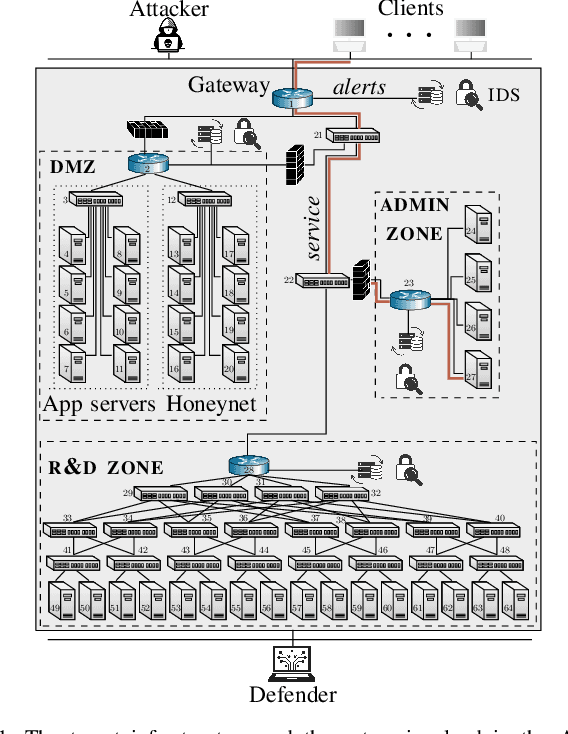
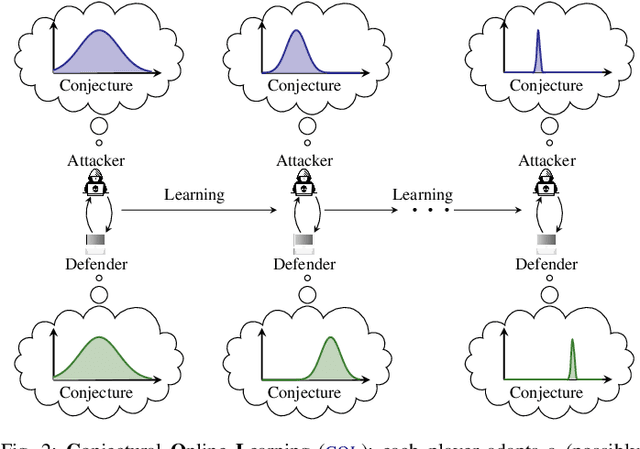
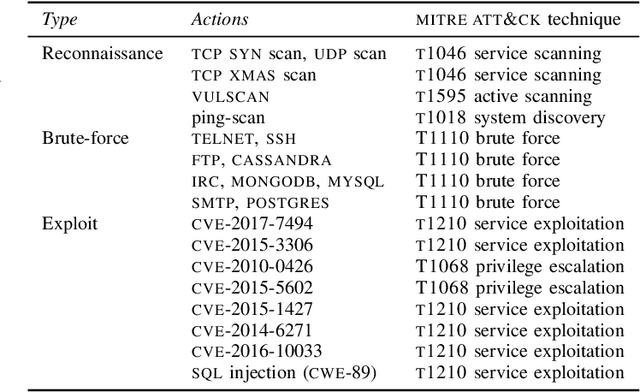
We study automated security response for an IT infrastructure and formulate the interaction between an attacker and a defender as a partially observed, non-stationary game. We relax the standard assumption that the game model is correctly specified and consider that each player has a probabilistic conjecture about the model, which may be misspecified in the sense that the true model has probability 0. This formulation allows us to capture uncertainty about the infrastructure and the intents of the players. To learn effective game strategies online, we design a novel method where a player iteratively adapts its conjecture using Bayesian learning and updates its strategy through rollout. We prove that the conjectures converge to best fits, and we provide a bound on the performance improvement that rollout enables with a conjectured model. To characterize the steady state of the game, we propose a variant of the Berk-Nash equilibrium. We present our method through an advanced persistent threat use case. Simulation studies based on testbed measurements show that our method produces effective security strategies that adapt to a changing environment. We also find that our method enables faster convergence than current reinforcement learning techniques.