Conjectural Online Learning with First-order Beliefs in Asymmetric Information Stochastic Games
Paper and Code
Mar 08, 2024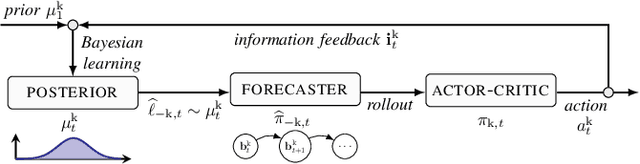

Asymmetric information stochastic games (\textsc{aisg}s) arise in many complex socio-technical systems, such as cyber-physical systems and IT infrastructures. Existing computational methods for \textsc{aisg}s are primarily offline and can not adapt to equilibrium deviations. Further, current methods are limited to special classes of \textsc{aisg}s to avoid belief hierarchies. To address these limitations, we propose conjectural online learning (\textsc{col}), an online method for generic \textsc{aisg}s. \textsc{col} uses a forecaster-actor-critic (\textsc{fac}) architecture where subjective forecasts are used to conjecture the opponents' strategies within a lookahead horizon, and Bayesian learning is used to calibrate the conjectures. To adapt strategies to nonstationary environments, \textsc{col} uses online rollout with cost function approximation (actor-critic). We prove that the conjectures produced by \textsc{col} are asymptotically consistent with the information feedback in the sense of a relaxed Bayesian consistency. We also prove that the empirical strategy profile induced by \textsc{col} converges to the Berk-Nash equilibrium, a solution concept characterizing rationality under subjectivity. Experimental results from an intrusion response use case demonstrate \textsc{col}'s superiority over state-of-the-art reinforcement learning methods against nonstationary attacks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge