ModelAngelo: Automated Model Building in Cryo-EM Maps

Electron cryo-microscopy (cryo-EM) produces three-dimensional (3D) maps of the electrostatic potential of biological macromolecules, including proteins. At sufficient resolution, the cryo-EM maps, along with some knowledge about the imaged molecules, allow de novo atomic modelling. Typically, this is done through a laborious manual process. Recent advances in machine learning applications to protein structure prediction show potential for automating this process. Taking inspiration from these techniques, we have built ModelAngelo for automated model building of proteins in cryo-EM maps. ModelAngelo first uses a residual convolutional neural network (CNN) to initialize a graph representation with nodes assigned to individual amino acids of the proteins in the map and edges representing the protein chain. The graph is then refined with a graph neural network (GNN) that combines the cryo-EM data, the amino acid sequence data and prior knowledge about protein geometries. The GNN refines the geometry of the protein chain and classifies the amino acids for each of its nodes. The final graph is post-processed with a hidden Markov model (HMM) search to map each protein chain to entries in a user provided sequence file. Application to 28 test cases shows that ModelAngelo outperforms the state-of-the-art and approximates manual building for cryo-EM maps with resolutions better than 3.5 \r{A}.

An Inductive Bias for Distances: Neural Nets that Respect the Triangle Inequality

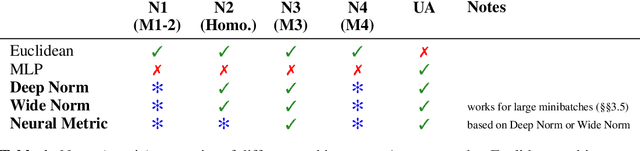
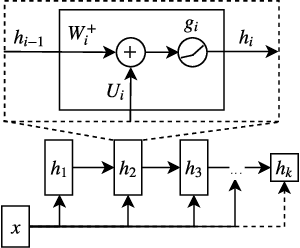
Distances are pervasive in machine learning. They serve as similarity measures, loss functions, and learning targets; it is said that a good distance measure solves a task. When defining distances, the triangle inequality has proven to be a useful constraint, both theoretically--to prove convergence and optimality guarantees--and empirically--as an inductive bias. Deep metric learning architectures that respect the triangle inequality rely, almost exclusively, on Euclidean distance in the latent space. Though effective, this fails to model two broad classes of subadditive distances, common in graphs and reinforcement learning: asymmetric metrics, and metrics that cannot be embedded into Euclidean space. To address these problems, we introduce novel architectures that are guaranteed to satisfy the triangle inequality. We prove our architectures universally approximate norm-induced metrics on $\mathbb{R}^n$, and present a similar result for modified Input Convex Neural Networks. We show that our architectures outperform existing metric approaches when modeling graph distances and have a better inductive bias than non-metric approaches when training data is limited in the multi-goal reinforcement learning setting.

DeepConsensus: using the consensus of features from multiple layers to attain robust image classification

We consider a classifier whose test set is exposed to various perturbations that are not present in the training set. These test samples still contain enough features to map them to the same class as their unperturbed counterpart. Current architectures exhibit rapid degradation of accuracy when trained on standard datasets but then used to classify perturbed samples of that data. To address this, we present a novel architecture named DeepConsensus that significantly improves generalization to these test-time perturbations. Our key insight is that deep neural networks should directly consider summaries of low and high level features when making classifications. Existing convolutional neural networks can be augmented with DeepConsensus, leading to improved resistance against large and small perturbations on MNIST, EMNIST, FashionMNIST, CIFAR10 and SVHN datasets.

ChainGAN: A sequential approach to GANs

We propose a new architecture and training methodology for generative adversarial networks. Current approaches attempt to learn the transformation from a noise sample to a generated data sample in one shot. Our proposed generator architecture, called $\textit{ChainGAN}$, uses a two-step process. It first attempts to transform a noise vector into a crude sample, similar to a traditional generator. Next, a chain of networks, called $\textit{editors}$, attempt to sequentially enhance this sample. We train each of these units independently, instead of with end-to-end backpropagation on the entire chain. Our model is robust, efficient, and flexible as we can apply it to various network architectures. We provide rationale for our choices and experimentally evaluate our model, achieving competitive results on several datasets.