Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Kfir Y Levy
Evaluating GANs via Duality
Nov 13, 2018Authors:Paulina Grnarova, Kfir Y Levy, Aurelien Lucchi, Nathanael Perraudin, Thomas Hofmann, Andreas Krause
Figures and Tables: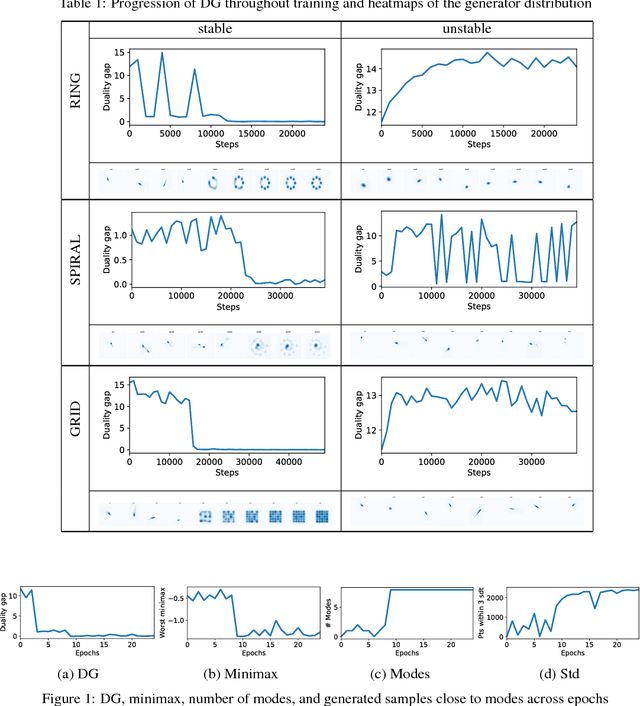
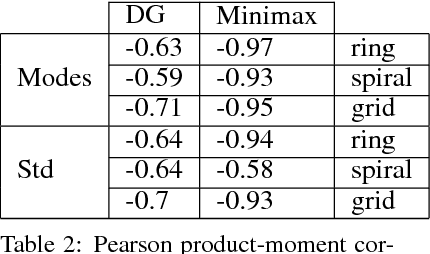
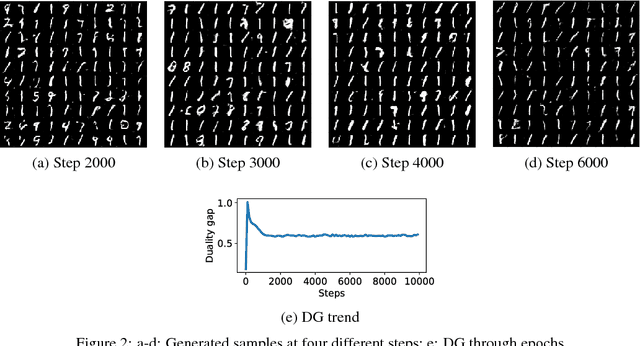
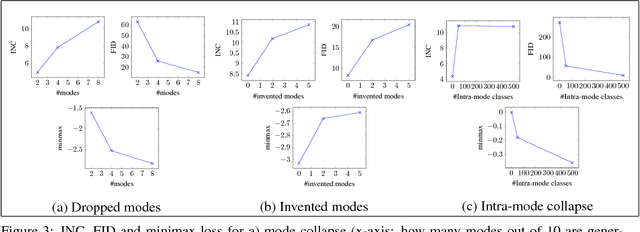




Abstract:Generative Adversarial Networks (GANs) have shown great results in accurately modeling complex distributions, but their training is known to be difficult due to instabilities caused by a challenging minimax optimization problem. This is especially troublesome given the lack of an evaluation metric that can reliably detect non-convergent behaviors. We leverage the notion of duality gap from game theory in order to propose a novel convergence metric for GANs that has low computational cost. We verify the validity of the proposed metric for various test scenarios commonly used in the literature.
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge