VertiSync: A Traffic Management Policy with Maximum Throughput for On-Demand Urban Air Mobility Networks

Urban Air Mobility (UAM) offers a solution to current traffic congestion by providing on-demand air mobility in urban areas. Effective traffic management is crucial for efficient operation of UAM systems, especially for high-demand scenarios. In this paper, we present VertiSync, a centralized traffic management policy for on-demand UAM networks. VertiSync schedules the aircraft for either servicing trip requests or rebalancing in the network subject to aircraft safety margins and separation requirements during takeoff and landing. We characterize the system-level throughput of VertiSync, which determines the demand threshold at which travel times transition from being stabilized to being increasing over time. We show that the proposed policy is able to maximize the throughput for sufficiently large fleet sizes. We demonstrate the performance of VertiSync through a case study for the city of Los Angeles. We show that VertiSync significantly reduces travel times compared to a first-come first-serve scheduling policy.

An Experimental Study on Learning Correlated Equilibrium in Routing Games

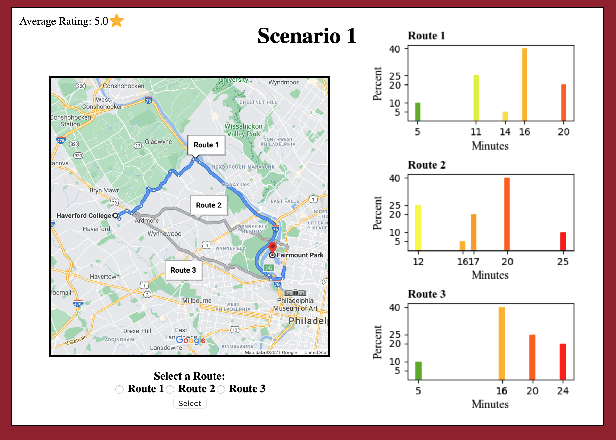
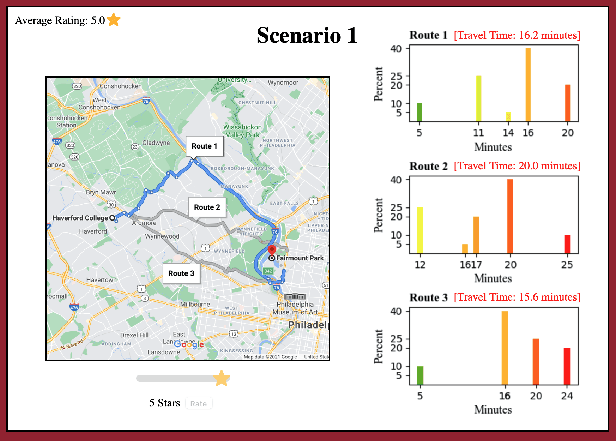
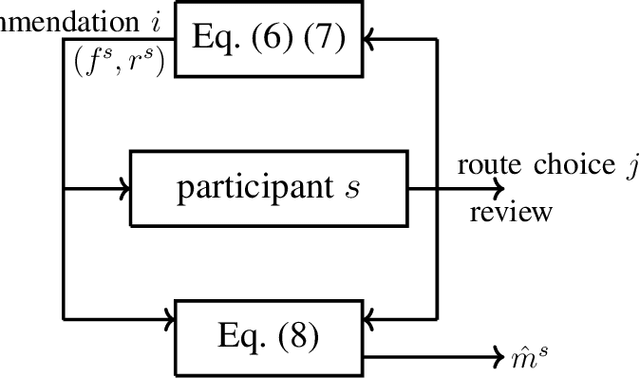
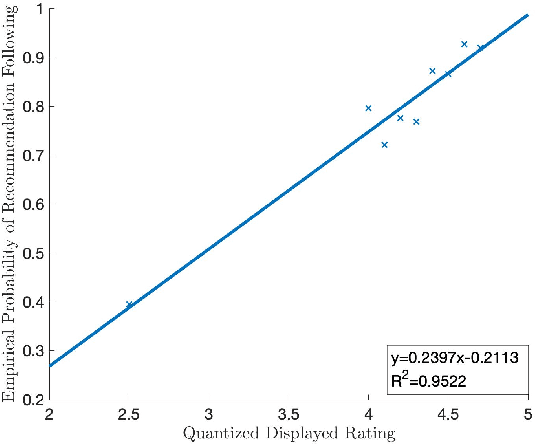
We study route choice in a repeated routing game where an uncertain state of nature determines link latency functions, and agents receive private route recommendation. The state is sampled in an i.i.d. manner in every round from a publicly known distribution, and the recommendations are generated by a randomization policy whose mapping from the state is known publicly. In a one-shot setting, the agents are said to obey recommendation if it gives the smallest travel time in a posteriori expectation. A plausible extension to repeated setting is that the likelihood of following recommendation in a round is related to regret from previous rounds. If the regret is of satisficing type with respect to a default choice and is averaged over past rounds and over all agents, then the asymptotic outcome under an obedient recommendation policy coincides with the one-shot outcome. We report findings from an experiment with one participant at a time engaged in repeated route choice decision on computer. In every round, the participant is shown travel time distribution for each route, a route recommendation generated by an obedient policy, and a rating suggestive of average experience of previous participants with the quality of recommendation. Upon entering route choice, the actual travel times are revealed. The participant evaluates the quality of recommendation by submitting a review. This is combined with historical reviews to update rating for the next round. Data analysis from 33 participants each with 100 rounds suggests moderate negative correlation between the display rating and the average regret, and a strong positive correlation between the rating and the likelihood of following recommendation. Overall, under obedient recommendation policy, the rating converges close to its maximum value by the end of the experiments in conjunction with very high frequency of following recommendations.

Saturation region of Freeway Networks under Safe Microscopic Ramp Metering

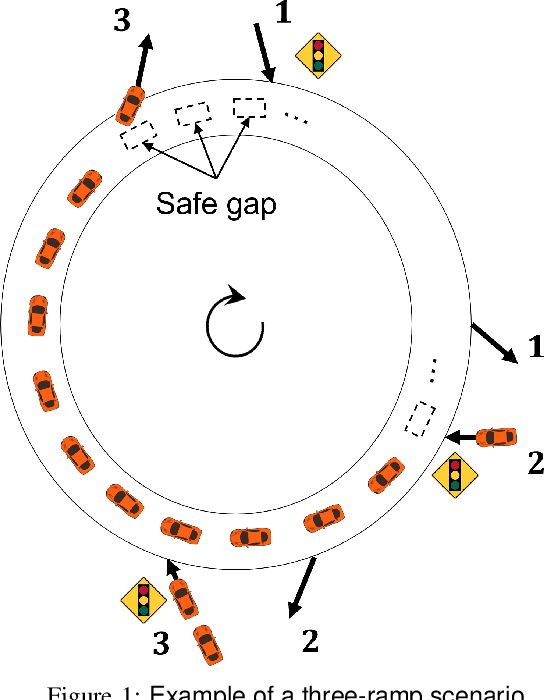
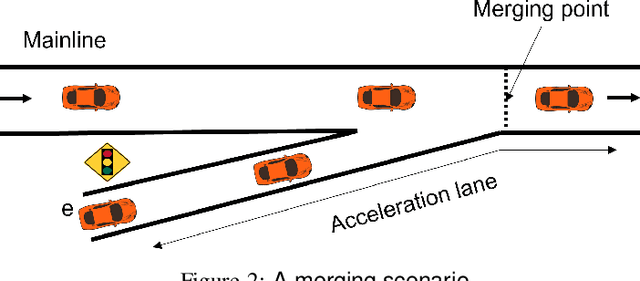
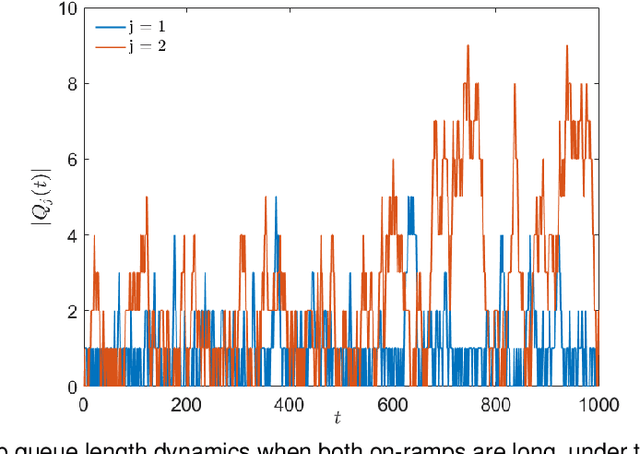
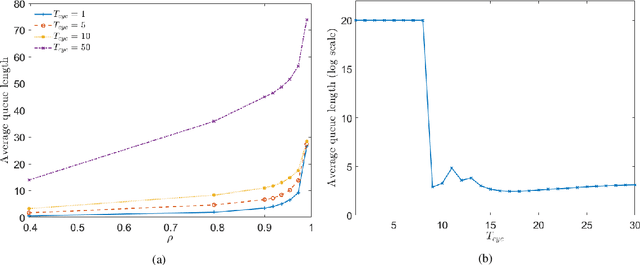
We consider ramp metering at the microscopic level subject to vehicle safety constraint. The traffic network is abstracted by a ring road with multiple on- and off-ramps. The arrival times of vehicles to the on-ramps, as well as their destination off-ramps are modeled by exogenous stochastic processes. Once a vehicle is released from an on-ramp, it accelerates towards the free flow speed if it is not obstructed by another vehicle; once it gets close to another vehicle, it adopts a safe behavior. The vehicle exits the traffic network once it reaches its destination off-ramp. We design traffic-responsive ramp metering policies which maximize the saturation region of the network. The saturation region of a policy is defined as the set of demands, i.e., arrival rates and the routing matrix, for which the queue lengths at all the on-ramps remain bounded in expectation. The proposed ramp metering policies operate under synchronous cycles during which an on-ramp does not release more vehicles than its queue length at the beginning of the cycle. We provide three policies under which, respectively, each on-ramp (i) pauses release for a time-interval at the end of the cycle, or (ii) modulates the release rate during the cycle, or (iii) adopts a conservative safety criterion for release during the cycle. None of the policies, however, require information about the demand. The saturation region of these policies is characterized by studying stochastic stability of the induced Markov chains, and is proven to be maximal when the merging speed of all on-ramps equals the free flow speed. Simulations are provided to illustrate the performance of the policies.

On Endogenous Reconfiguration in Mobile Robotic Networks

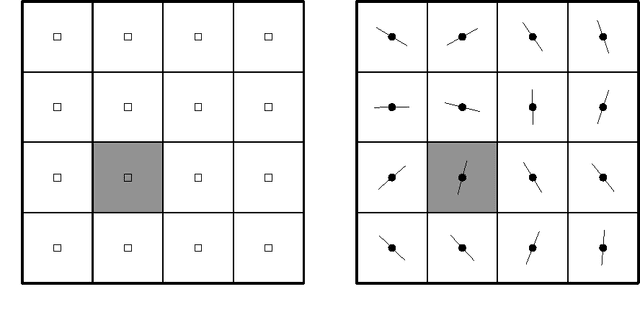
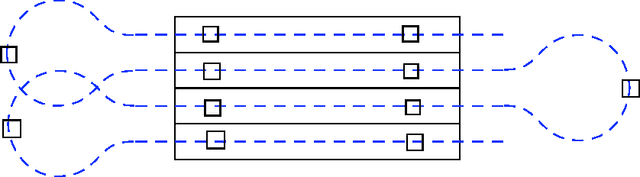
In this paper, our focus is on certain applications for mobile robotic networks, where reconfiguration is driven by factors intrinsic to the network rather than changes in the external environment. In particular, we study a version of the coverage problem useful for surveillance applications, where the objective is to position the robots in order to minimize the average distance from a random point in a given environment to the closest robot. This problem has been well-studied for omni-directional robots and it is shown that optimal configuration for the network is a centroidal Voronoi configuration and that the coverage cost belongs to $\Theta(m^{-1/2})$, where $m$ is the number of robots in the network. In this paper, we study this problem for more realistic models of robots, namely the double integrator (DI) model and the differential drive (DD) model. We observe that the introduction of these motion constraints in the algorithm design problem gives rise to an interesting behavior. For a \emph{sparser} network, the optimal algorithm for these models of robots mimics that for omni-directional robots. We propose novel algorithms whose performances are within a constant factor of the optimal asymptotically (i.e., as $m \to +\infty$). In particular, we prove that the coverage cost for the DI and DD models of robots is of order $m^{-1/3}$. Additionally, we show that, as the network grows, these novel algorithms outperform the conventional algorithm; hence necessitating a reconfiguration in the network in order to maintain optimal quality of service.

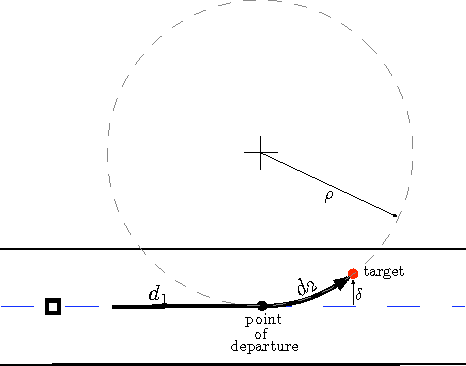
Traveing Salesperson Problems for a double integrator

In this paper we propose some novel path planning strategies for a double integrator with bounded velocity and bounded control inputs. First, we study the following version of the Traveling Salesperson Problem (TSP): given a set of points in $\real^d$, find the fastest tour over the point set for a double integrator. We first give asymptotic bounds on the time taken to complete such a tour in the worst-case. Then, we study a stochastic version of the TSP for double integrator where the points are randomly sampled from a uniform distribution in a compact environment in $\real^2$ and $\real^3$. We propose novel algorithms that perform within a constant factor of the optimal strategy with high probability. Lastly, we study a dynamic TSP: given a stochastic process that generates targets, is there a policy which guarantees that the number of unvisited targets does not diverge over time? If such stable policies exist, what is the minimum wait for a target? We propose novel stabilizing receding-horizon algorithms whose performances are within a constant factor from the optimum with high probability, in $\real^2$ as well as $\real^3$. We also argue that these algorithms give identical performances for a particular nonholonomic vehicle, Dubins vehicle.

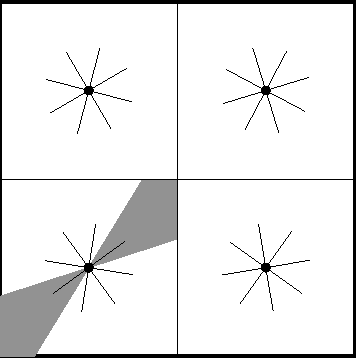
Asymptotic constant-factor approximation algorithm for the Traveling Salesperson Problem for Dubins' vehicle

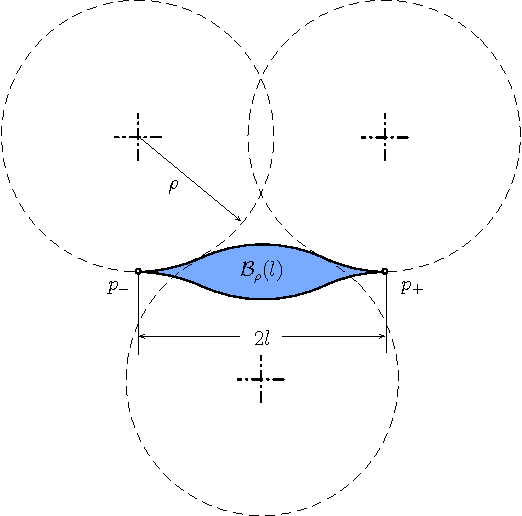
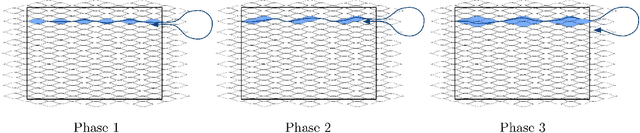
This article proposes the first known algorithm that achieves a constant-factor approximation of the minimum length tour for a Dubins' vehicle through $n$ points on the plane. By Dubins' vehicle, we mean a vehicle constrained to move at constant speed along paths with bounded curvature without reversing direction. For this version of the classic Traveling Salesperson Problem, our algorithm closes the gap between previously established lower and upper bounds; the achievable performance is of order $n^{2/3}$.