Saturation region of Freeway Networks under Safe Microscopic Ramp Metering
Paper and Code
Jul 05, 2022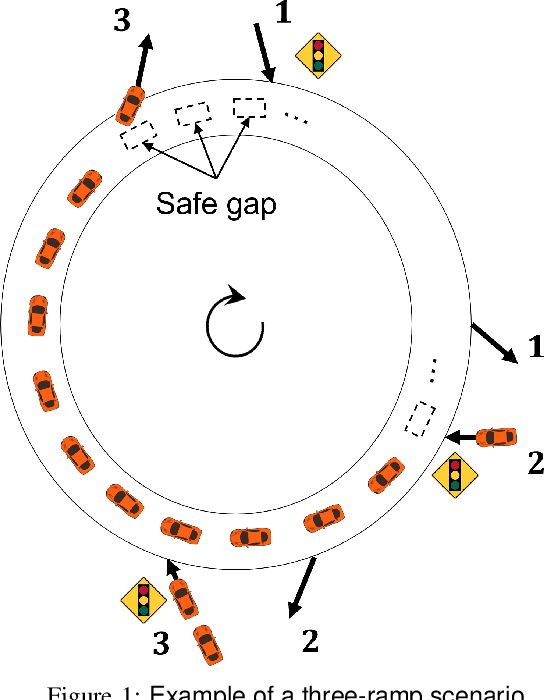
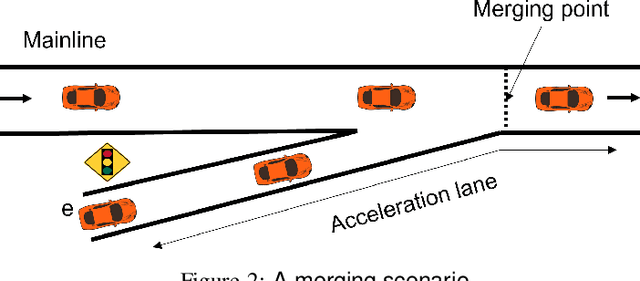
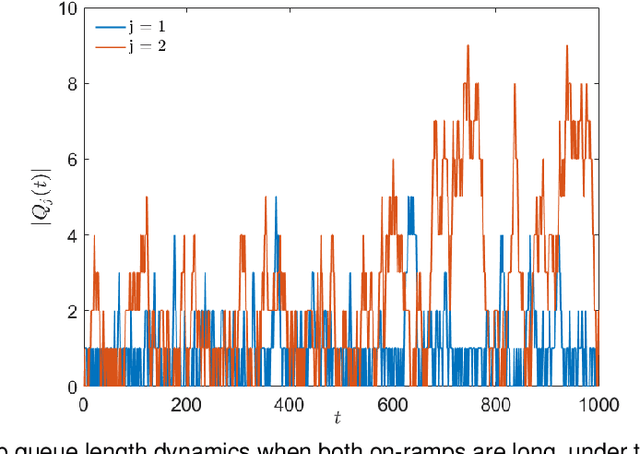
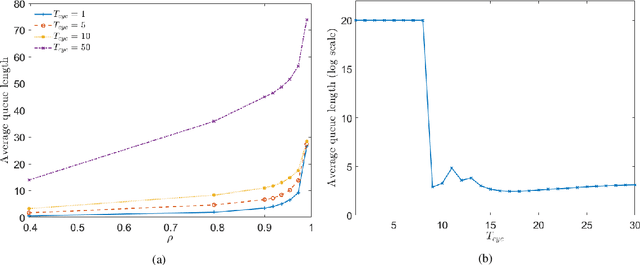
We consider ramp metering at the microscopic level subject to vehicle safety constraint. The traffic network is abstracted by a ring road with multiple on- and off-ramps. The arrival times of vehicles to the on-ramps, as well as their destination off-ramps are modeled by exogenous stochastic processes. Once a vehicle is released from an on-ramp, it accelerates towards the free flow speed if it is not obstructed by another vehicle; once it gets close to another vehicle, it adopts a safe behavior. The vehicle exits the traffic network once it reaches its destination off-ramp. We design traffic-responsive ramp metering policies which maximize the saturation region of the network. The saturation region of a policy is defined as the set of demands, i.e., arrival rates and the routing matrix, for which the queue lengths at all the on-ramps remain bounded in expectation. The proposed ramp metering policies operate under synchronous cycles during which an on-ramp does not release more vehicles than its queue length at the beginning of the cycle. We provide three policies under which, respectively, each on-ramp (i) pauses release for a time-interval at the end of the cycle, or (ii) modulates the release rate during the cycle, or (iii) adopts a conservative safety criterion for release during the cycle. None of the policies, however, require information about the demand. The saturation region of these policies is characterized by studying stochastic stability of the induced Markov chains, and is proven to be maximal when the merging speed of all on-ramps equals the free flow speed. Simulations are provided to illustrate the performance of the policies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge