On Endogenous Reconfiguration in Mobile Robotic Networks
Paper and Code
Jul 18, 2008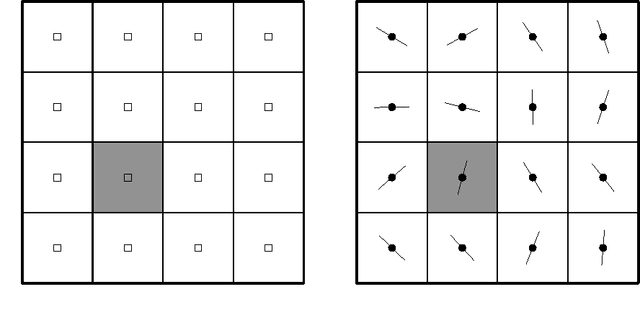
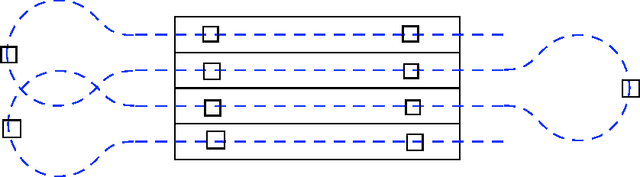
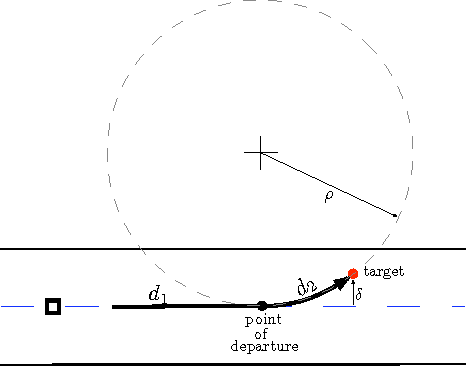
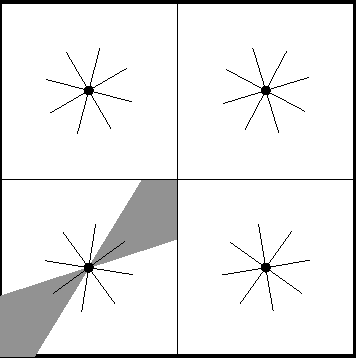
In this paper, our focus is on certain applications for mobile robotic networks, where reconfiguration is driven by factors intrinsic to the network rather than changes in the external environment. In particular, we study a version of the coverage problem useful for surveillance applications, where the objective is to position the robots in order to minimize the average distance from a random point in a given environment to the closest robot. This problem has been well-studied for omni-directional robots and it is shown that optimal configuration for the network is a centroidal Voronoi configuration and that the coverage cost belongs to $\Theta(m^{-1/2})$, where $m$ is the number of robots in the network. In this paper, we study this problem for more realistic models of robots, namely the double integrator (DI) model and the differential drive (DD) model. We observe that the introduction of these motion constraints in the algorithm design problem gives rise to an interesting behavior. For a \emph{sparser} network, the optimal algorithm for these models of robots mimics that for omni-directional robots. We propose novel algorithms whose performances are within a constant factor of the optimal asymptotically (i.e., as $m \to +\infty$). In particular, we prove that the coverage cost for the DI and DD models of robots is of order $m^{-1/3}$. Additionally, we show that, as the network grows, these novel algorithms outperform the conventional algorithm; hence necessitating a reconfiguration in the network in order to maintain optimal quality of service.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge