Traveing Salesperson Problems for a double integrator
Paper and Code
Sep 17, 2006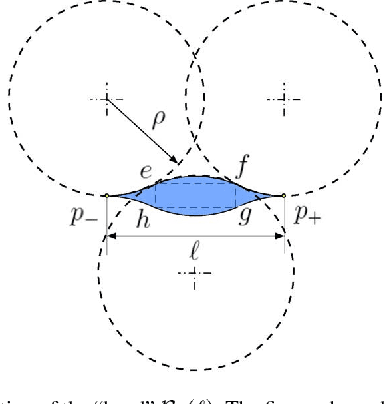
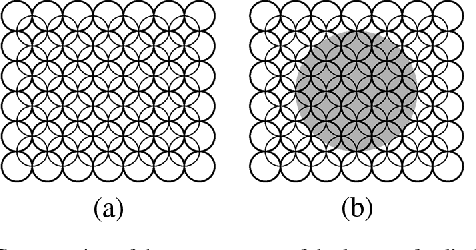
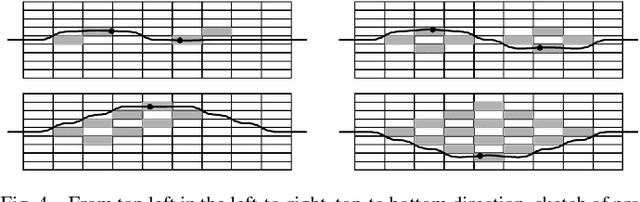
In this paper we propose some novel path planning strategies for a double integrator with bounded velocity and bounded control inputs. First, we study the following version of the Traveling Salesperson Problem (TSP): given a set of points in $\real^d$, find the fastest tour over the point set for a double integrator. We first give asymptotic bounds on the time taken to complete such a tour in the worst-case. Then, we study a stochastic version of the TSP for double integrator where the points are randomly sampled from a uniform distribution in a compact environment in $\real^2$ and $\real^3$. We propose novel algorithms that perform within a constant factor of the optimal strategy with high probability. Lastly, we study a dynamic TSP: given a stochastic process that generates targets, is there a policy which guarantees that the number of unvisited targets does not diverge over time? If such stable policies exist, what is the minimum wait for a target? We propose novel stabilizing receding-horizon algorithms whose performances are within a constant factor from the optimum with high probability, in $\real^2$ as well as $\real^3$. We also argue that these algorithms give identical performances for a particular nonholonomic vehicle, Dubins vehicle.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge