Kozuchi Agent: A Language-Agnostic Open-Weight Agent for Software Repair

Industrial software-engineering teams increasingly need LLM agents that turn bug reports into correct patches, yet benchmark-scale operation adds long horizons, tool-use discipline, context persistence, heterogeneous clusters, and evaluation reuse. We present Kozuchi Agent, a language-agnostic open-weight repair agent and CI-operated evaluation pipeline. Explicit phases, persistent state, deterministic tools, a model-independent action interface, and cross-agent test-time selection make runs auditable and repeatable. With locally hosted Qwen3.5-27B, no fine-tuning, and TTS@8, Kozuchi resolves 374/500 SWE-bench Verified instances on the official evaluator. Unchanged on Multi-SWE-bench Java, the same 27-billion-parameter agent resolves 41/128 instances (32.03%), ranking first among strict open-weight submissions and fourth of 42 overall; on Python it ranks 12th of 135 and first among open-weight systems. Per-phase behavior remains within +/-5 percentage points across languages. Remaining failures mainly reflect semantic correctness, Java-specific harness issues, and selection errors. Across both tracks, results compare favorably with open/local peers by parameter count. Analysis of candidate diversity, selector regret, and patch reliability shows that the remaining gap is primarily semantic correctness and selection rather than edit formatting or proprietary-model access. Operationally, reusable CI stages reduce operator touch-points from five to one across heterogeneous internal clusters.

Adaptive Targeted Dynamic Chunking for Tokenization-Free Hierarchical Model

Tokenization-free hierarchical models are emerging as a promising alternative to traditional Large Language Models (LLMs), addressing inherent preprocessing issues such as vocabulary design complexity, out-of-vocabulary (OOV) errors, and language-specific constraints. However, a significant challenge in these byte-level methods is the optimization of the compression ratio, a critical factor that dictates model performance for processing bytes data via chunks. In this paper, we propose Adaptive Targeted Dynamic Chunking (ATDC), a novel byte-compression control mechanism designed to enhance the effectiveness of dynamic chunking within hierarchical architectures. Our approach utilizes curriculum learning to progressively adjust the compression ratio during training, transitioning from low to high compression to stabilize the learning process. We provide an analysis establishing the relationship between the target compression ratio and Bytes-Per-Innermost-Chunk (BPIC), allowing for tracking of chunk-size evolution throughout the training phase. Evaluations conducted on the FineWeb-Edu 100B dataset demonstrate that hierarchical models equipped with ATDC achieve competitive Bits-Per-Byte (BPB) performance compared to conventional baselines operating at both byte and token levels. Furthermore, the proposed method exhibits more stable training dynamics and superior final performance across diverse downstream tasks compared to models using fixed compression ratios, while maintaining the inherent robustness and flexibility of byte-level processing.

Direct Quantized Training of Language Models with Stochastic Rounding

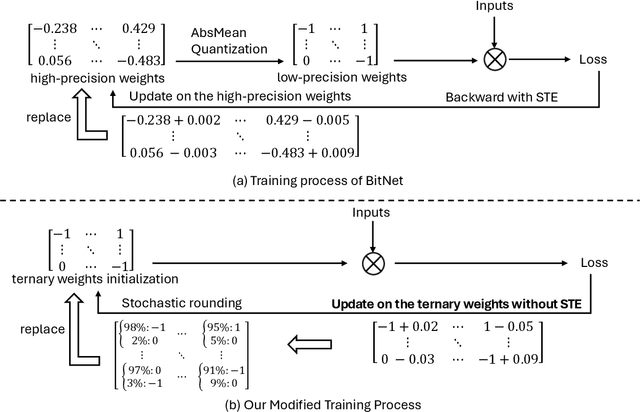
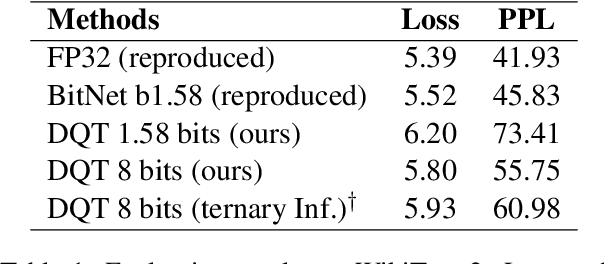
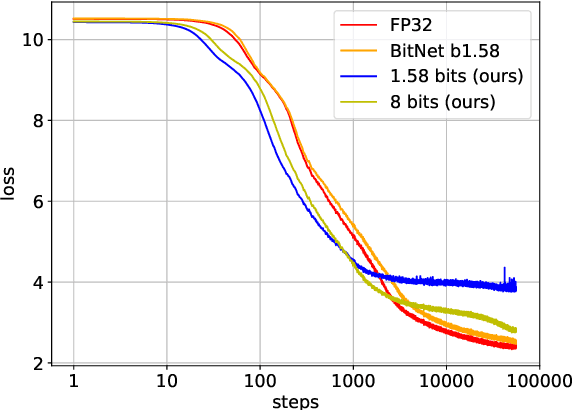
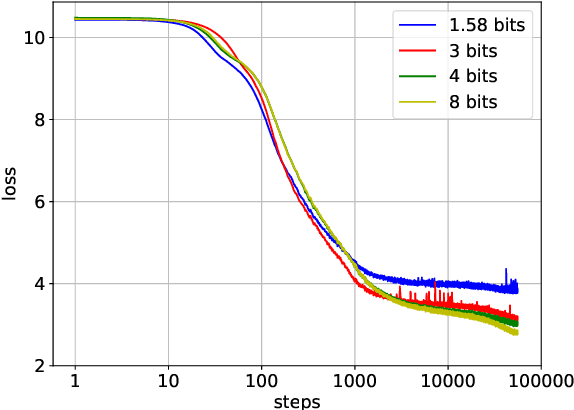
Although recent quantized Large Language Models (LLMs), such as BitNet, have paved the way for significant reduction in memory usage during deployment with binary or ternary weights, training these models still demands substantial memory footprints. This is partly because high-precision (i.e., unquantized) weight matrices required for straight-through estimation must be maintained throughout the whole training process. To address this, we explore the potential of directly updating the quantized low-precision weight matrices without relying on the straight-through estimator during backpropagation, thereby saving memory usage during training. Specifically, we employ a stochastic rounding technique to minimize information loss caused by the use of low-bit weights throughout training. Experimental results on our LLaMA-structured models indicate that (1) training with only low-precision weights is feasible even when they are constrained to ternary values, (2) extending the bit width to 8 bits results in only a 5% loss degradation compared to BitNet b1.58 while offering the potential for reduced memory usage during training, and (3) our models can also perform inference using ternary weights, showcasing their flexibility in deployment.

Neural Network Module Decomposition and Recomposition

We propose a modularization method that decomposes a deep neural network (DNN) into small modules from a functionality perspective and recomposes them into a new model for some other task. Decomposed modules are expected to have the advantages of interpretability and verifiability due to their small size. In contrast to existing studies based on reusing models that involve retraining, such as a transfer learning model, the proposed method does not require retraining and has wide applicability as it can be easily combined with existing functional modules. The proposed method extracts modules using weight masks and can be applied to arbitrary DNNs. Unlike existing studies, it requires no assumption about the network architecture. To extract modules, we designed a learning method and a loss function to maximize shared weights among modules. As a result, the extracted modules can be recomposed without a large increase in the size. We demonstrate that the proposed method can decompose and recompose DNNs with high compression ratio and high accuracy and is superior to the existing method through sharing weights between modules.