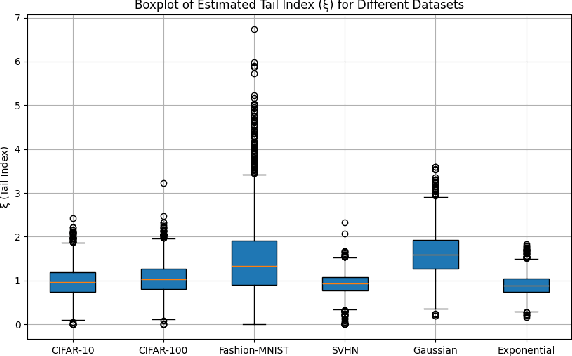
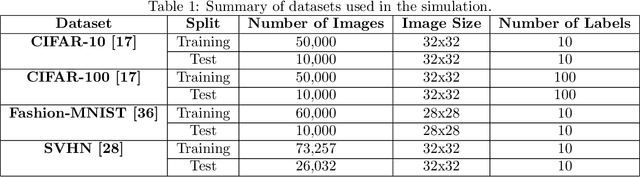
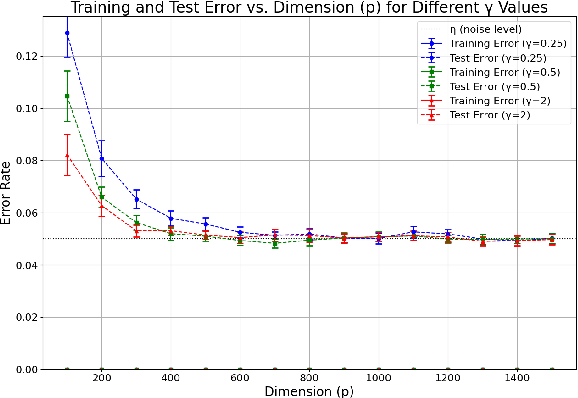
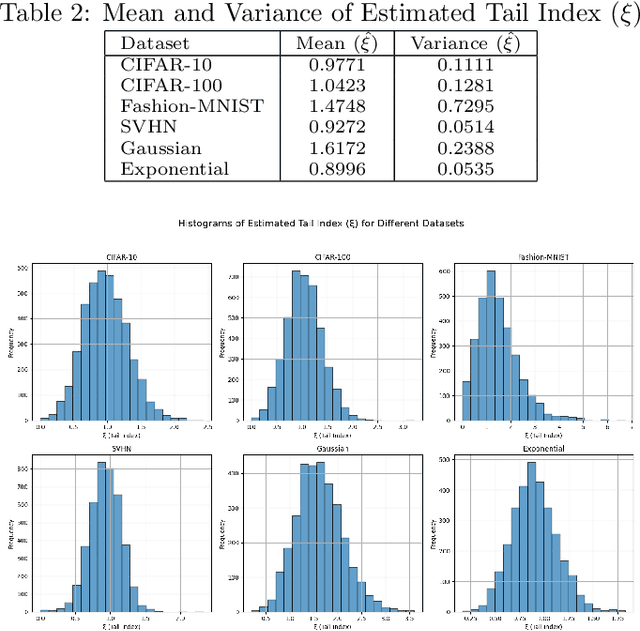
Benign Overfitting for $α$ Sub-exponential Input

This paper investigates the phenomenon of benign overfitting in binary classification problems with heavy-tailed input distributions. We extend the analysis of maximum margin classifiers to $\alpha$ sub-exponential distributions, where $\alpha \in (0,2]$, generalizing previous work that focused on sub-gaussian inputs. Our main result provides generalization error bounds for linear classifiers trained using gradient descent on unregularized logistic loss in this heavy-tailed setting. We prove that under certain conditions on the dimensionality $p$ and feature vector magnitude $\|\mu\|$, the misclassification error of the maximum margin classifier asymptotically approaches the noise level. This work contributes to the understanding of benign overfitting in more robust distribution settings and demonstrates that the phenomenon persists even with heavier-tailed inputs than previously studied.

Enhancing Hierarchical Information by Using Metric Cones for Graph Embedding

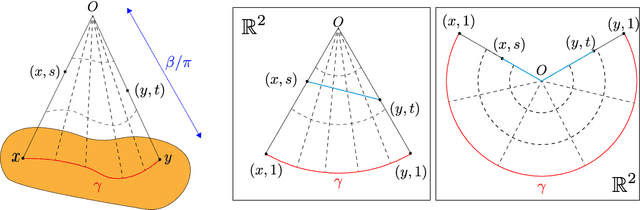
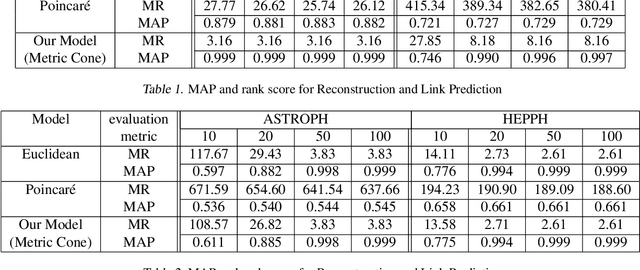
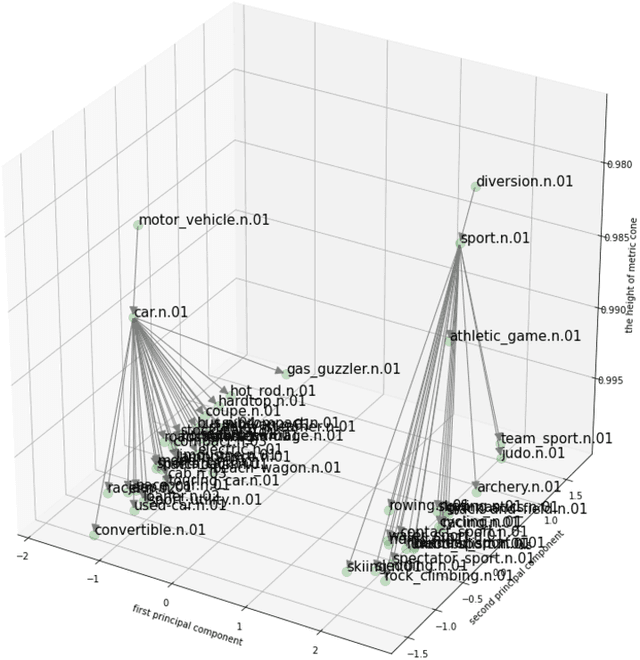
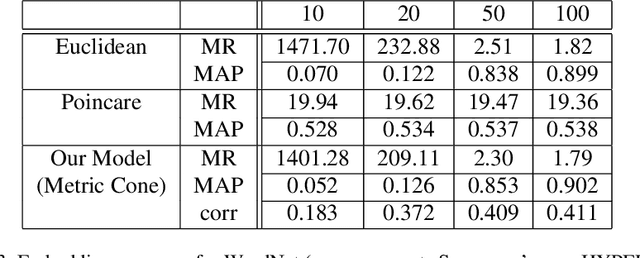
Graph embedding is becoming an important method with applications in various areas, including social networks and knowledge graph completion. In particular, Poincar\'e embedding has been proposed to capture the hierarchical structure of graphs, and its effectiveness has been reported. However, most of the existing methods have isometric mappings in the embedding space, and the choice of the origin point can be arbitrary. This fact is not desirable when the distance from the origin is used as an indicator of hierarchy, as in the case of Poincar\'e embedding. In this paper, we propose graph embedding in a metric cone to solve such a problem, and we gain further benefits: 1) we provide an indicator of hierarchical information that is both geometrically and intuitively natural to interpret, 2) we can extract the hierarchical structure from a graph embedding output of other methods by learning additional one-dimensional parameters, and 3) we can change the curvature of the embedding space via a hyperparameter.

Why is the Mahalanobis Distance Effective for Anomaly Detection?

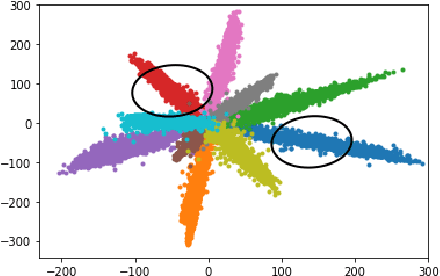
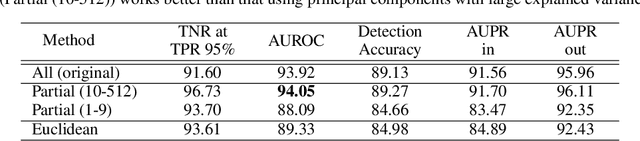
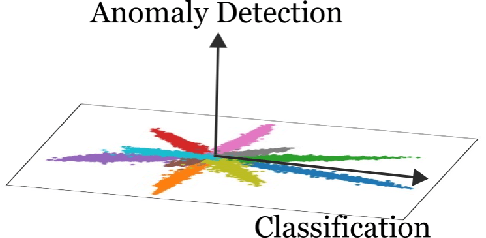
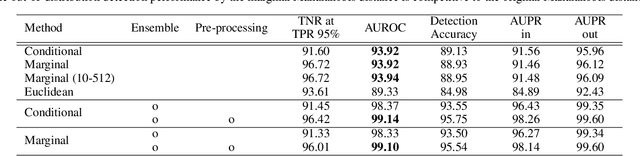
The Mahalanobis distance-based confidence score, a recently proposed anomaly detection method for pre-trained neural classifiers, achieves state-of-the-art performance on both out-of-distribution and adversarial example detection. This work analyzes why this method exhibits such strong performance while imposing an implausible assumption; namely, that class conditional distributions of intermediate features have tied covariance. We reveal that the reason for its effectiveness has been misunderstood. Although this method scores the prediction confidence for the original classification task, our analysis suggests that information critical for classification task does not contribute to state-of-the-art performance on anomaly detection. To support this hypothesis, we demonstrate that a simpler confidence score that does not use class information is as effective as the original method in most cases. Moreover, our experiments show that the confidence scores can exhibit different behavior on other frameworks such as metric learning models, and their detection performance is sensitive to model architecture choice. These findings provide insight into the behavior of neural classifiers when provided with anomalous inputs.

Likelihood Assignment for Out-of-Distribution Inputs in Deep Generative Models is Sensitive to Prior Distribution Choice

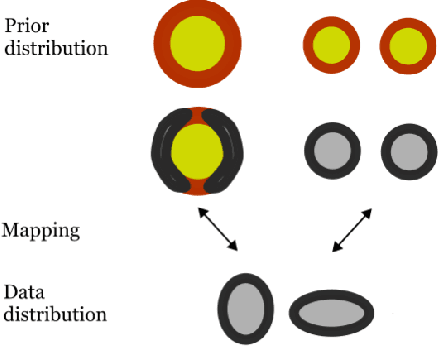
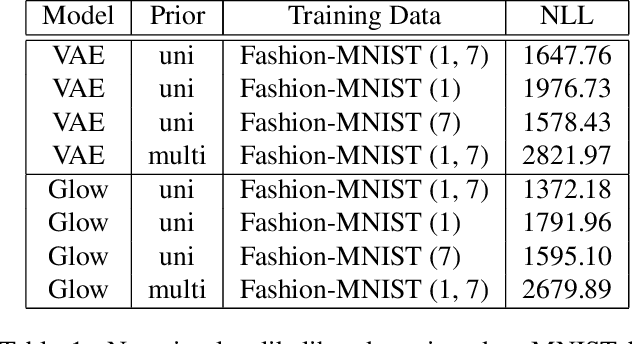
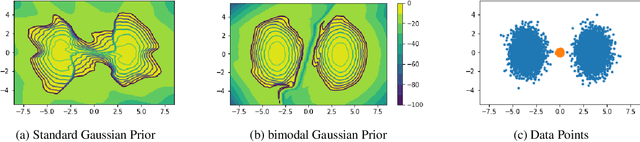
Recent work has shown that deep generative models assign higher likelihood to out-of-distribution inputs than to training data. We show that a factor underlying this phenomenon is a mismatch between the nature of the prior distribution and that of the data distribution, a problem found in widely used deep generative models such as VAEs and Glow. While a typical choice for a prior distribution is a standard Gaussian distribution, properties of distributions of real data sets may not be consistent with a unimodal prior distribution. This paper focuses on the relationship between the choice of a prior distribution and the likelihoods assigned to out-of-distribution inputs. We propose the use of a mixture distribution as a prior to make likelihoods assigned by deep generative models sensitive to out-of-distribution inputs. Furthermore, we explain the theoretical advantages of adopting a mixture distribution as the prior, and we present experimental results to support our claims. Finally, we demonstrate that a mixture prior lowers the out-of-distribution likelihood with respect to two pairs of real image data sets: Fashion-MNIST vs. MNIST and CIFAR10 vs. SVHN.

Revisiting the Vector Space Model: Sparse Weighted Nearest-Neighbor Method for Extreme Multi-Label Classification

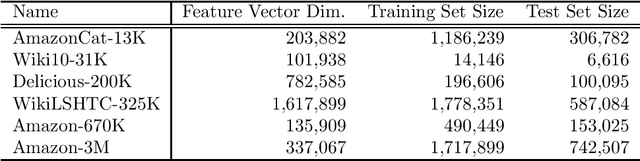
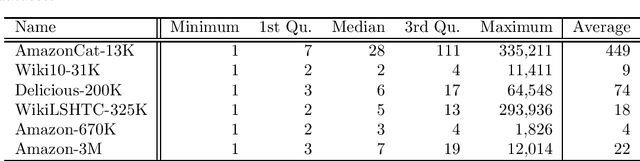
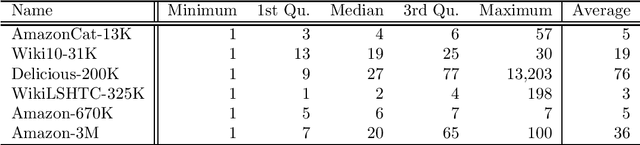
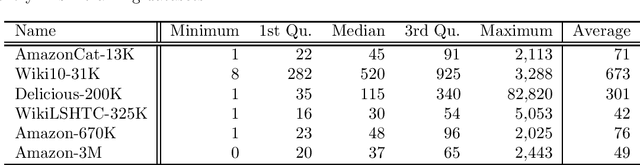
Machine learning has played an important role in information retrieval (IR) in recent times. In search engines, for example, query keywords are accepted and documents are returned in order of relevance to the given query; this can be cast as a multi-label ranking problem in machine learning. Generally, the number of candidate documents is extremely large (from several thousand to several million); thus, the classifier must handle many labels. This problem is referred to as extreme multi-label classification (XMLC). In this paper, we propose a novel approach to XMLC termed the Sparse Weighted Nearest-Neighbor Method. This technique can be derived as a fast implementation of state-of-the-art (SOTA) one-versus-rest linear classifiers for very sparse datasets. In addition, we show that the classifier can be written as a sparse generalization of a representer theorem with a linear kernel. Furthermore, our method can be viewed as the vector space model used in IR. Finally, we show that the Sparse Weighted Nearest-Neighbor Method can process data points in real time on XMLC datasets with equivalent performance to SOTA models, with a single thread and smaller storage footprint. In particular, our method exhibits superior performance to the SOTA models on a dataset with 3 million labels.