Revisiting the Vector Space Model: Sparse Weighted Nearest-Neighbor Method for Extreme Multi-Label Classification
Paper and Code
Feb 12, 2018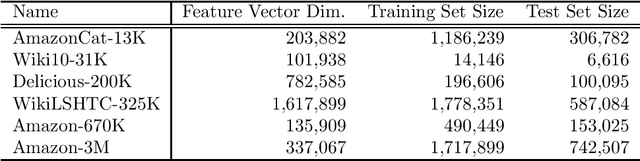
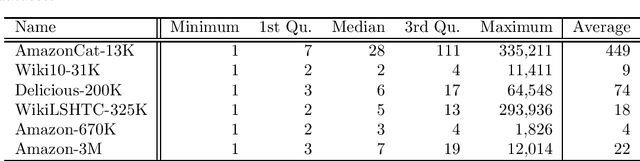
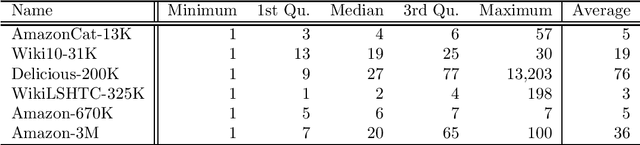
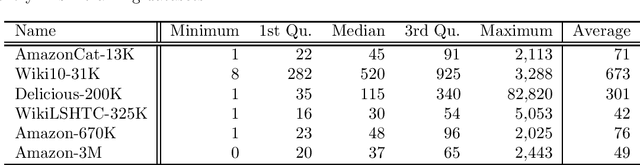
Machine learning has played an important role in information retrieval (IR) in recent times. In search engines, for example, query keywords are accepted and documents are returned in order of relevance to the given query; this can be cast as a multi-label ranking problem in machine learning. Generally, the number of candidate documents is extremely large (from several thousand to several million); thus, the classifier must handle many labels. This problem is referred to as extreme multi-label classification (XMLC). In this paper, we propose a novel approach to XMLC termed the Sparse Weighted Nearest-Neighbor Method. This technique can be derived as a fast implementation of state-of-the-art (SOTA) one-versus-rest linear classifiers for very sparse datasets. In addition, we show that the classifier can be written as a sparse generalization of a representer theorem with a linear kernel. Furthermore, our method can be viewed as the vector space model used in IR. Finally, we show that the Sparse Weighted Nearest-Neighbor Method can process data points in real time on XMLC datasets with equivalent performance to SOTA models, with a single thread and smaller storage footprint. In particular, our method exhibits superior performance to the SOTA models on a dataset with 3 million labels.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge