Enhancing Hierarchical Information by Using Metric Cones for Graph Embedding
Paper and Code
Feb 16, 2021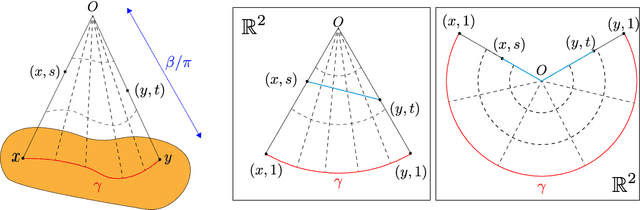
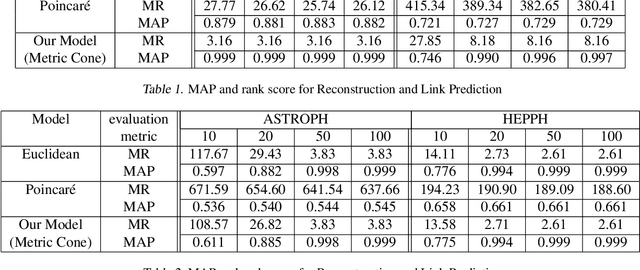
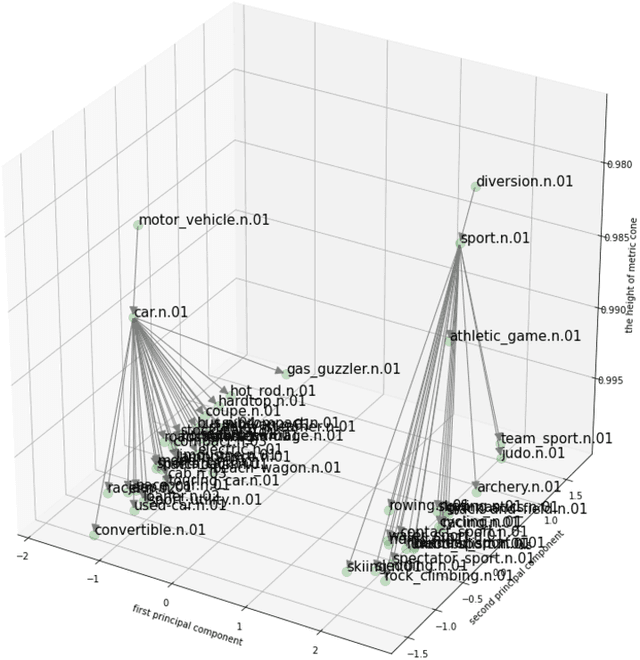
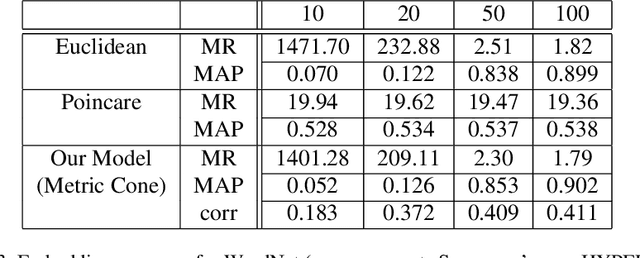
Graph embedding is becoming an important method with applications in various areas, including social networks and knowledge graph completion. In particular, Poincar\'e embedding has been proposed to capture the hierarchical structure of graphs, and its effectiveness has been reported. However, most of the existing methods have isometric mappings in the embedding space, and the choice of the origin point can be arbitrary. This fact is not desirable when the distance from the origin is used as an indicator of hierarchy, as in the case of Poincar\'e embedding. In this paper, we propose graph embedding in a metric cone to solve such a problem, and we gain further benefits: 1) we provide an indicator of hierarchical information that is both geometrically and intuitively natural to interpret, 2) we can extract the hierarchical structure from a graph embedding output of other methods by learning additional one-dimensional parameters, and 3) we can change the curvature of the embedding space via a hyperparameter.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge