Why is the Mahalanobis Distance Effective for Anomaly Detection?

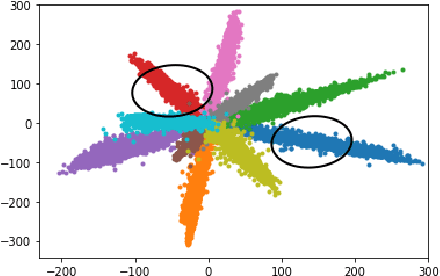
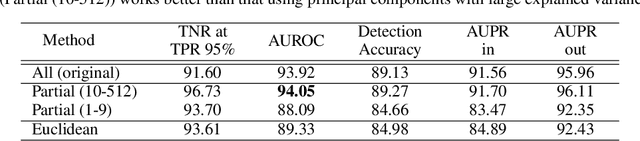
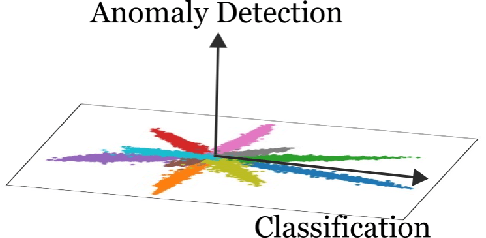
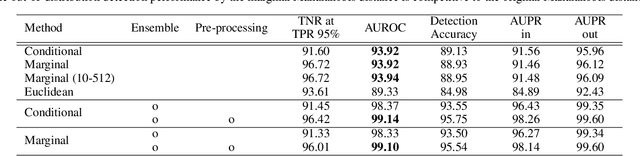
The Mahalanobis distance-based confidence score, a recently proposed anomaly detection method for pre-trained neural classifiers, achieves state-of-the-art performance on both out-of-distribution and adversarial example detection. This work analyzes why this method exhibits such strong performance while imposing an implausible assumption; namely, that class conditional distributions of intermediate features have tied covariance. We reveal that the reason for its effectiveness has been misunderstood. Although this method scores the prediction confidence for the original classification task, our analysis suggests that information critical for classification task does not contribute to state-of-the-art performance on anomaly detection. To support this hypothesis, we demonstrate that a simpler confidence score that does not use class information is as effective as the original method in most cases. Moreover, our experiments show that the confidence scores can exhibit different behavior on other frameworks such as metric learning models, and their detection performance is sensitive to model architecture choice. These findings provide insight into the behavior of neural classifiers when provided with anomalous inputs.