Haptic Perception via the Dynamics of Flexible Body Inspired by an Ostrich's Neck

In biological systems, haptic perception is achieved through both flexible skin and flexible body. In fully soft robots, the fragility of their bodies and the time delays in sensory processing pose significant challenges. The musculoskeletal system possesses both the deformability inherent in soft materials and the durability of rigid-body robots. Additionally, by outsourcing part of the intelligent information processing to the morphology of the musculoskeletal system, applications for dynamic tasks are expected. This study focuses on the pecking movements of birds, which achieve precise haptic perception through the musculoskeletal system of their flexible neck. Physical reservoir computing is applied to flexible structures inspired by an ostrich neck to analyze the relationship between haptic perception and physical characteristics. Combined experiments using both an actual robot and simulations demonstrate that, under appropriate body viscoelasticity, the flexible structure can distinguish objects of varying softness and memorize this information as behaviors. Drawing on these findings and anatomical insights from the ostrich neck, a haptic sensing system is proposed that possesses separability and this behavioral memory in flexible structures, enabling rapid learning and real-time inference. The results demonstrate that through the dynamics of flexible structures, diverse functions can emerge beyond their original design as manipulators.

Training Spiking Neural Networks via Augmented Direct Feedback Alignment

Spiking neural networks (SNNs), the models inspired by the mechanisms of real neurons in the brain, transmit and represent information by employing discrete action potentials or spikes. The sparse, asynchronous properties of information processing make SNNs highly energy efficient, leading to SNNs being promising solutions for implementing neural networks in neuromorphic devices. However, the nondifferentiable nature of SNN neurons makes it a challenge to train them. The current training methods of SNNs that are based on error backpropagation (BP) and precisely designing surrogate gradient are difficult to implement and biologically implausible, hindering the implementation of SNNs on neuromorphic devices. Thus, it is important to train SNNs with a method that is both physically implementatable and biologically plausible. In this paper, we propose using augmented direct feedback alignment (aDFA), a gradient-free approach based on random projection, to train SNNs. This method requires only partial information of the forward process during training, so it is easy to implement and biologically plausible. We systematically demonstrate the feasibility of the proposed aDFA-SNNs scheme, propose its effective working range, and analyze its well-performing settings by employing genetic algorithm. We also analyze the impact of crucial features of SNNs on the scheme, thus demonstrating its superiority and stability over BP and conventional direct feedback alignment. Our scheme can achieve competitive performance without accurate prior knowledge about the utilized system, thus providing a valuable reference for physically training SNNs.

Transient Chaos in BERT

Language is an outcome of our complex and dynamic human-interactions and the technique of natural language processing (NLP) is hence built on human linguistic activities. Bidirectional Encoder Representations from Transformers (BERT) has recently gained its popularity by establishing the state-of-the-art scores in several NLP benchmarks. A Lite BERT (ALBERT) is literally characterized as a lightweight version of BERT, in which the number of BERT parameters is reduced by repeatedly applying the same neural network called Transformer's encoder layer. By pre-training the parameters with a massive amount of natural language data, ALBERT can convert input sentences into versatile high-dimensional vectors potentially capable of solving multiple NLP tasks. In that sense, ALBERT can be regarded as a well-designed high-dimensional dynamical system whose operator is the Transformer's encoder, and essential structures of human language are thus expected to be encapsulated in its dynamics. In this study, we investigated the embedded properties of ALBERT to reveal how NLP tasks are effectively solved by exploiting its dynamics. We thereby aimed to explore the nature of human language from the dynamical expressions of the NLP model. Our short-term analysis clarified that the pre-trained model stably yields trajectories with higher dimensionality, which would enhance the expressive capacity required for NLP tasks. Also, our long-term analysis revealed that ALBERT intrinsically shows transient chaos, a typical nonlinear phenomenon showing chaotic dynamics only in its transient, and the pre-trained ALBERT model tends to produce the chaotic trajectory for a significantly longer time period compared to a randomly-initialized one. Our results imply that local chaoticity would contribute to improving NLP performance, uncovering a novel aspect in the role of chaotic dynamics in human language behaviors.

Designing spontaneous behavioral switching via chaotic itinerancy

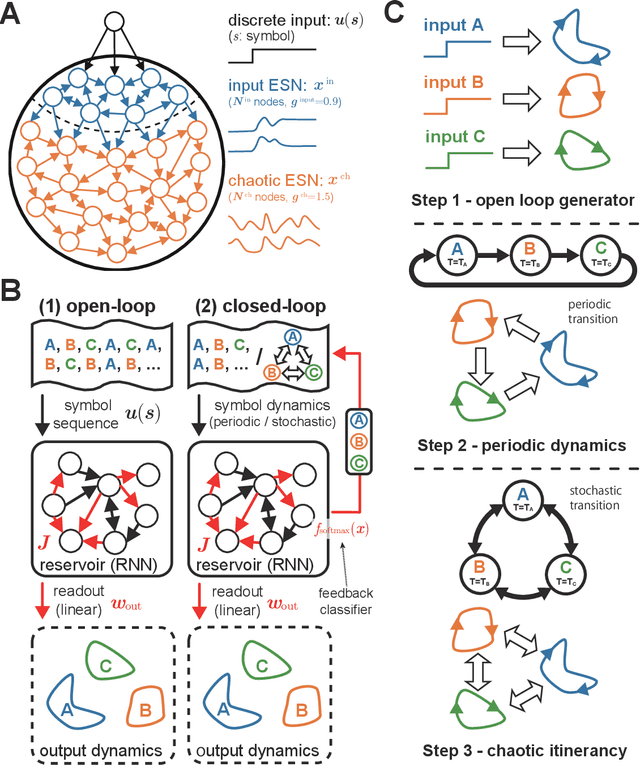
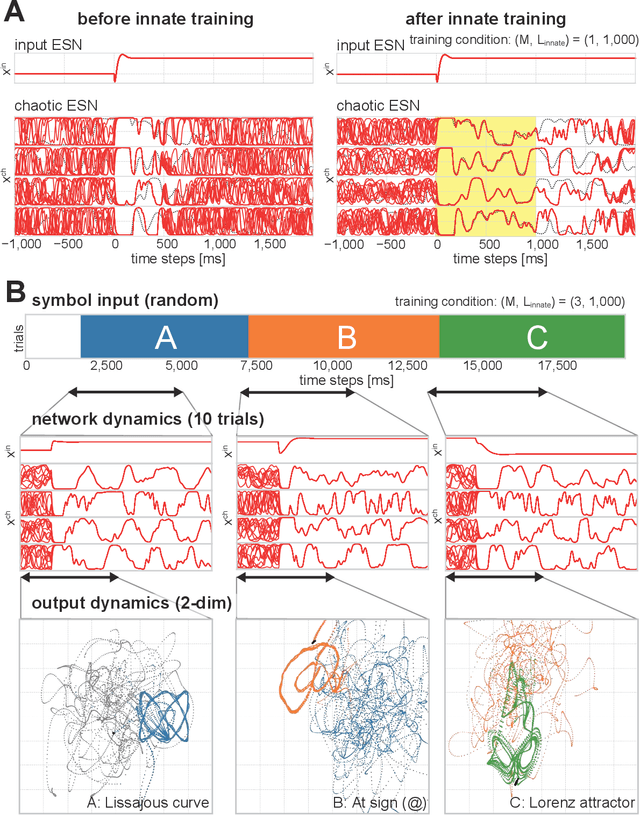
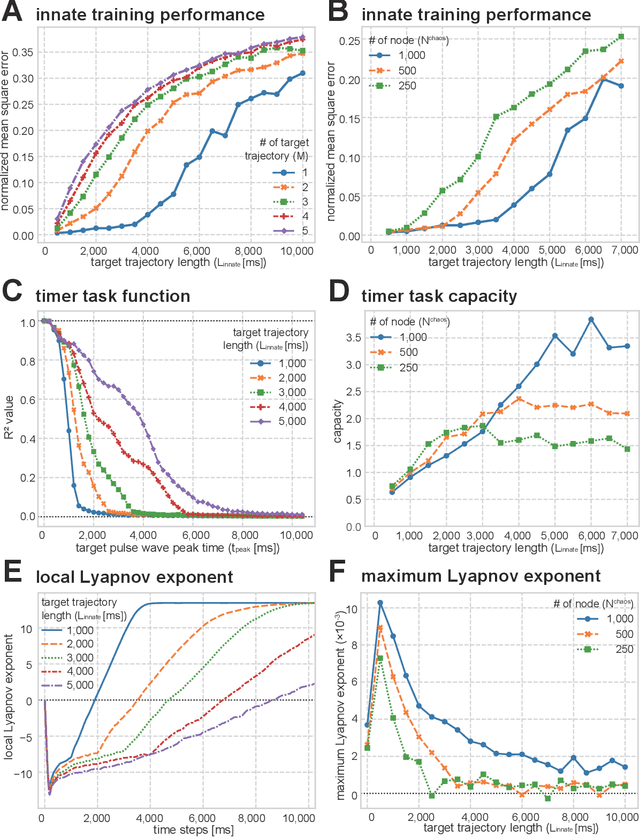
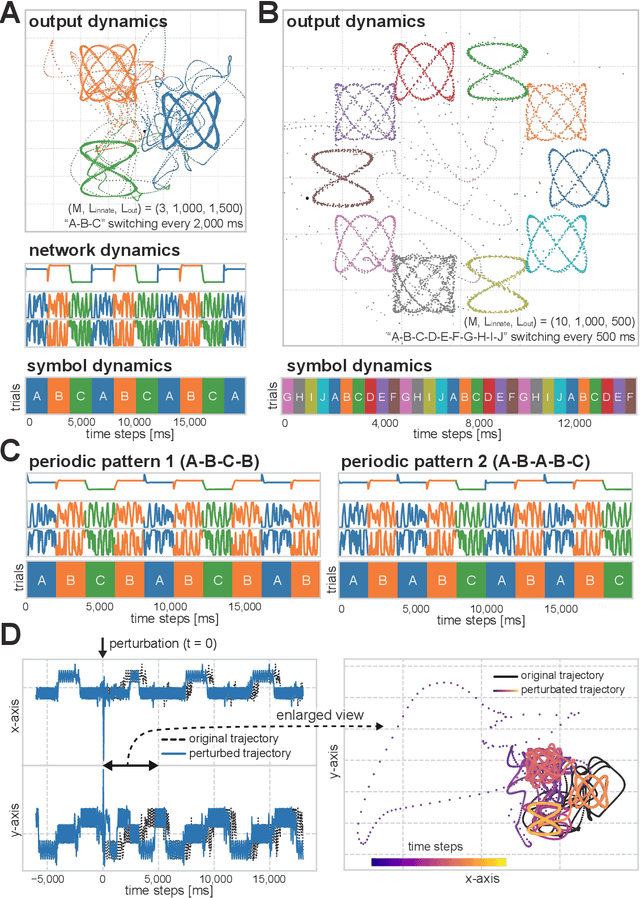
Chaotic itinerancy is a frequently observed phenomenon in high-dimensional and nonlinear dynamical systems, and it is characterized by the random transitions among multiple quasi-attractors. Several studies have revealed that chaotic itinerancy has been observed in brain activity, and it is considered to play a critical role in the spontaneous, stable behavior generation of animals. Thus, chaotic itinerancy is a topic of great interest, particularly for neurorobotics researchers who wish to understand and implement autonomous behavioral controls for agents. However, it is generally difficult to gain control over high-dimensional nonlinear dynamical systems. Hence, the implementation of chaotic itinerancy has mainly been accomplished heuristically. In this study, we propose a novel way of implementing chaotic itinerancy reproducibly and at will in a generic high-dimensional chaotic system. In particular, we demonstrate that our method enables us to easily design both the trajectories of quasi-attractors and the transition rules among them simply by adjusting the limited number of system parameters and by utilizing the intrinsic high-dimensional chaos. Finally, we quantitatively discuss the validity and scope of application through the results of several numerical experiments.