Unsupervised clustering of series using dynamic programming and neural processes

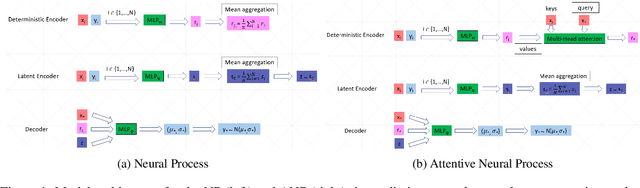
Following the work of arXiv:2101.09512, we are interested in clustering a given multi-variate series in an unsupervised manner. We would like to segment and cluster the series such that the resulting blocks present in each cluster are coherent with respect to a predefined model structure (e.g. a physics model with a functional form defined by a number of parameters). However, such approach might have its limitation, partly because there may exist multiple models that describe the same data, and partly because the exact model behind the data may not immediately known. Hence, it is useful to establish a general framework that enables the integration of plausible models and also accommodates data-driven approach into one approximated model to assist the clustering task. Hence, in this work, we investigate the use of neural processes to build the approximated model while yielding the same assumptions required by the algorithm presented in arXiv:2101.09512.

Unsupervised clustering of series using dynamic programming

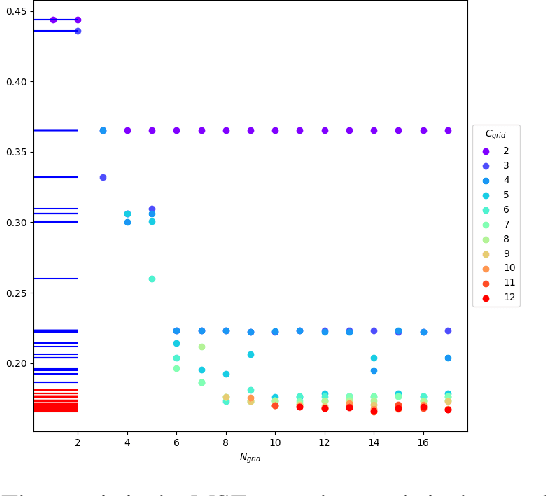
We are interested in clustering parts of a given single multi-variate series in an unsupervised manner. We would like to segment and cluster the series such that the resulting blocks present in each cluster are coherent with respect to a known model (e.g. physics model). Data points are said to be coherent if they can be described using this model with the same parameters. We have designed an algorithm based on dynamic programming with constraints on the number of clusters, the number of transitions as well as the minimal size of a block such that the clusters are coherent with this process. We present an use-case: clustering of petrophysical series using the Waxman-Smits equation.

Multi-task Reinforcement Learning with a Planning Quasi-Metric

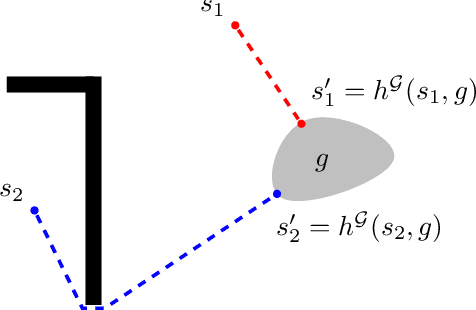
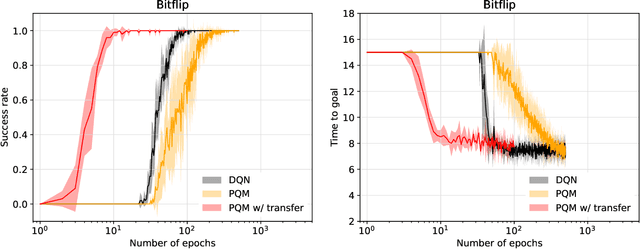
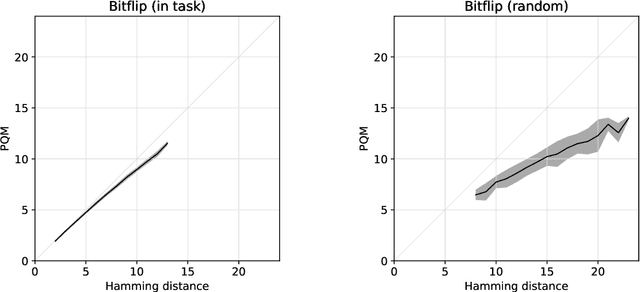
We introduce a new reinforcement learning approach combining a planning quasi-metric (PQM) that estimates the number of actions required to go from a state to another, with task-specific planners that compute a target state to reach a given goal. The main advantage of this decomposition is to allow the sharing across tasks of a task-agnostic model of the quasi-metric that captures the environment's dynamics and can be learned in a dense and unsupervised manner. We demonstrate the usefulness of this approach on the standard bit-flip problem and in the MuJoCo robotic arm simulator.