Chang-Yu Hou
Unsupervised clustering of series using dynamic programming and neural processes
Jan 26, 2021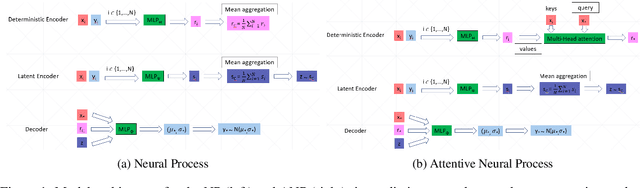



Abstract:Following the work of arXiv:2101.09512, we are interested in clustering a given multi-variate series in an unsupervised manner. We would like to segment and cluster the series such that the resulting blocks present in each cluster are coherent with respect to a predefined model structure (e.g. a physics model with a functional form defined by a number of parameters). However, such approach might have its limitation, partly because there may exist multiple models that describe the same data, and partly because the exact model behind the data may not immediately known. Hence, it is useful to establish a general framework that enables the integration of plausible models and also accommodates data-driven approach into one approximated model to assist the clustering task. Hence, in this work, we investigate the use of neural processes to build the approximated model while yielding the same assumptions required by the algorithm presented in arXiv:2101.09512.
Unsupervised clustering of series using dynamic programming
Jan 23, 2021


Abstract:We are interested in clustering parts of a given single multi-variate series in an unsupervised manner. We would like to segment and cluster the series such that the resulting blocks present in each cluster are coherent with respect to a known model (e.g. physics model). Data points are said to be coherent if they can be described using this model with the same parameters. We have designed an algorithm based on dynamic programming with constraints on the number of clusters, the number of transitions as well as the minimal size of a block such that the clusters are coherent with this process. We present an use-case: clustering of petrophysical series using the Waxman-Smits equation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge