Unsupervised clustering of series using dynamic programming and neural processes

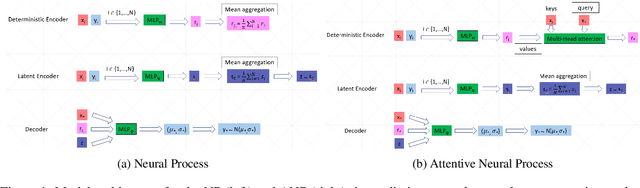
Following the work of arXiv:2101.09512, we are interested in clustering a given multi-variate series in an unsupervised manner. We would like to segment and cluster the series such that the resulting blocks present in each cluster are coherent with respect to a predefined model structure (e.g. a physics model with a functional form defined by a number of parameters). However, such approach might have its limitation, partly because there may exist multiple models that describe the same data, and partly because the exact model behind the data may not immediately known. Hence, it is useful to establish a general framework that enables the integration of plausible models and also accommodates data-driven approach into one approximated model to assist the clustering task. Hence, in this work, we investigate the use of neural processes to build the approximated model while yielding the same assumptions required by the algorithm presented in arXiv:2101.09512.

Unsupervised clustering of series using dynamic programming

We are interested in clustering parts of a given single multi-variate series in an unsupervised manner. We would like to segment and cluster the series such that the resulting blocks present in each cluster are coherent with respect to a known model (e.g. physics model). Data points are said to be coherent if they can be described using this model with the same parameters. We have designed an algorithm based on dynamic programming with constraints on the number of clusters, the number of transitions as well as the minimal size of a block such that the clusters are coherent with this process. We present an use-case: clustering of petrophysical series using the Waxman-Smits equation.

Dual Neural Network Architecture for Determining Epistemic and Aleatoric Uncertainties

Deep learning techniques have been shown to be extremely effective for various classification and regression problems, but quantifying the uncertainty of their predictions and separating them into the epistemic and aleatoric fractions is still considered challenging. In oil and gas exploration projects, tools consisting of seismic, sonic, magnetic resonance, resistivity, dielectric and/or nuclear sensors are sent downhole through boreholes to probe the earth's rock and fluid properties. The measurements from these tools are used to build reservoir models that are subsequently used for estimation and optimization of hydrocarbon production. Machine learning algorithms are often used to estimate the rock and fluid properties from the measured downhole data. Quantifying uncertainties of these properties is crucial for rock and fluid evaluation and subsequent reservoir optimization and production decisions. These machine learning algorithms are often trained on a "ground-truth" or core database. During the inference phase which involves application of these algorithms to field data, it is critical that the machine learning algorithm flag data as out of distribution from new geologies that the model was not trained upon. It is also highly important to be sensitive to heteroscedastic aleatoric noise in the feature space arising from the combination of tool and geological conditions. Understanding the source of the uncertainty and reducing them is key to designing intelligent tools and applications such as automated log interpretation answer products for exploration and field development. In this paper we describe a methodology consisting of a system of dual networks comprising of the combination of a Bayesian Neural Network (BNN) and an Artificial Neural Network (ANN) addressing this challenge for geophysical applications.