What's Wrong with Deep Learning in Tree Search for Combinatorial Optimization

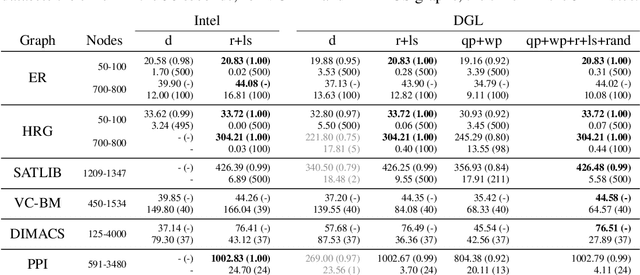
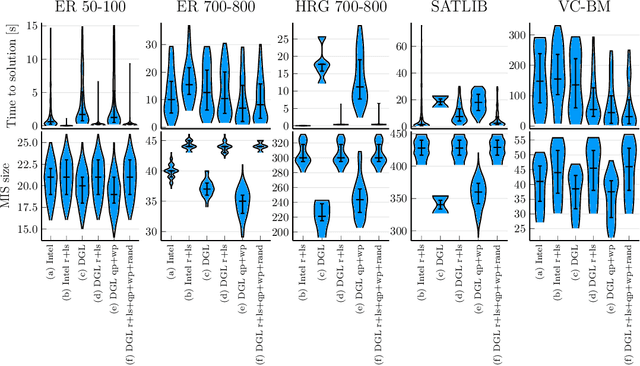
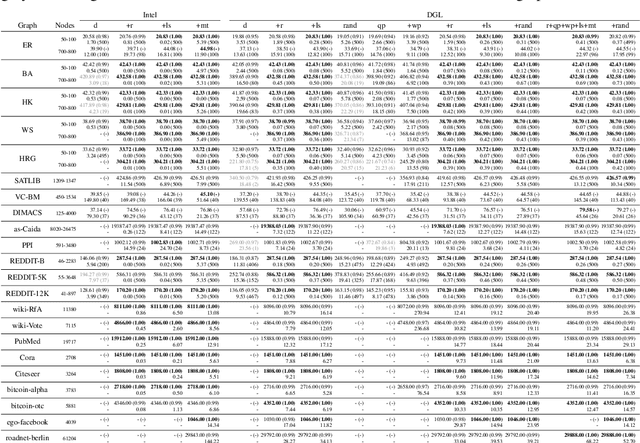
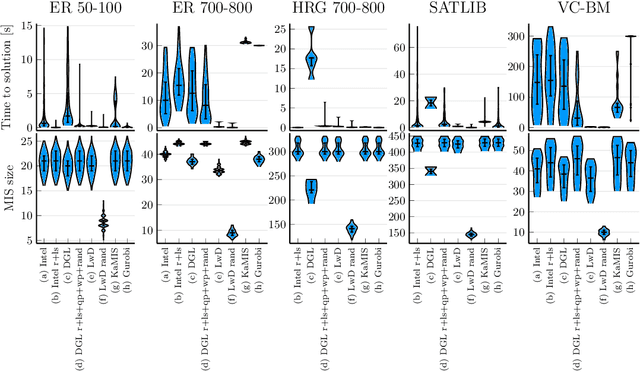
Combinatorial optimization lies at the core of many real-world problems. Especially since the rise of graph neural networks (GNNs), the deep learning community has been developing solvers that derive solutions to NP-hard problems by learning the problem-specific solution structure. However, reproducing the results of these publications proves to be difficult. We make three contributions. First, we present an open-source benchmark suite for the NP-hard Maximum Independent Set problem, in both its weighted and unweighted variants. The suite offers a unified interface to various state-of-the-art traditional and machine learning-based solvers. Second, using our benchmark suite, we conduct an in-depth analysis of the popular guided tree search algorithm by Li et al. [NeurIPS 2018], testing various configurations on small and large synthetic and real-world graphs. By re-implementing their algorithm with a focus on code quality and extensibility, we show that the graph convolution network used in the tree search does not learn a meaningful representation of the solution structure, and can in fact be replaced by random values. Instead, the tree search relies on algorithmic techniques like graph kernelization to find good solutions. Thus, the results from the original publication are not reproducible. Third, we extend the analysis to compare the tree search implementations to other solvers, showing that the classical algorithmic solvers often are faster, while providing solutions of similar quality. Additionally, we analyze a recent solver based on reinforcement learning and observe that for this solver, the GNN is responsible for the competitive solution quality.

Learning Languages in the Limit from Positive Information with Finitely Many Memory Changes

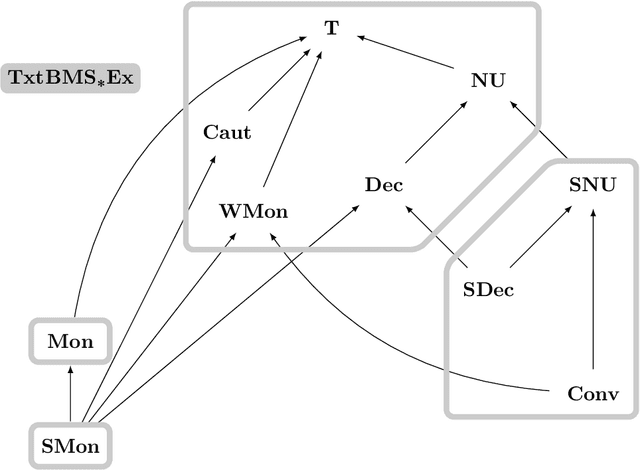
We investigate learning collections of languages from texts by an inductive inference machine with access to the current datum and its memory in form of states. The bounded memory states (BMS) learner is considered successful in case it eventually settles on a correct hypothesis while exploiting only finitely many different states. We give the complete map of all pairwise relations for an established collection of learning success restrictions. Most prominently, we show that non-U-shapedness is not restrictive, while conservativeness and (strong) monotonicity are. Some results carry over from iterative learning by a general lemma showing that, for a wealth of restrictions (the \emph{semantic} restrictions), iterative and bounded memory states learning are equivalent. We also give an example of a non-semantic restriction (strongly non-U-shapedness) where the two settings differ.

Learning Half-Spaces and other Concept Classes in the Limit with Iterative Learners

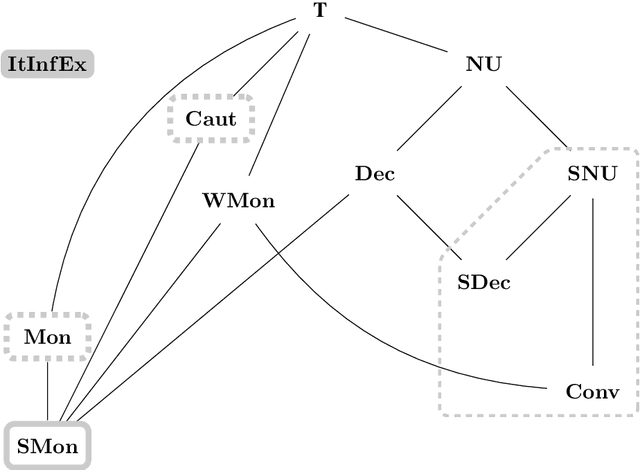
In order to model an efficient learning paradigm, iterative learning algorithms access data one by one, updating the current hypothesis without regress to past data. Past research on iterative learning analyzed for example many important additional requirements and their impact on iterative learners. In this paper, our results are twofold. First, we analyze the relative learning power of various settings of iterative learning, including learning from text and from informant, as well as various further restrictions, for example we show that strongly non-U-shaped learning is restrictive for iterative learning from informant. Second, we investigate the learnability of the concept class of half-spaces and provide a constructive iterative algorithm to learn the set of half-spaces from informant.

Learning from Informants: Relations between Learning Success Criteria

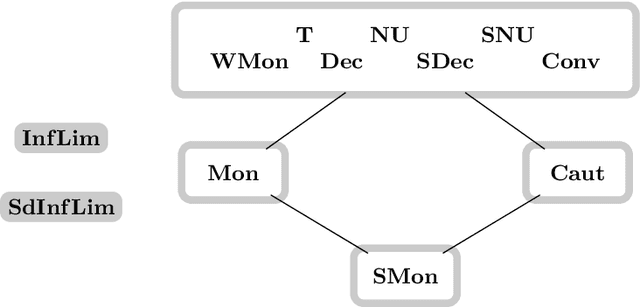
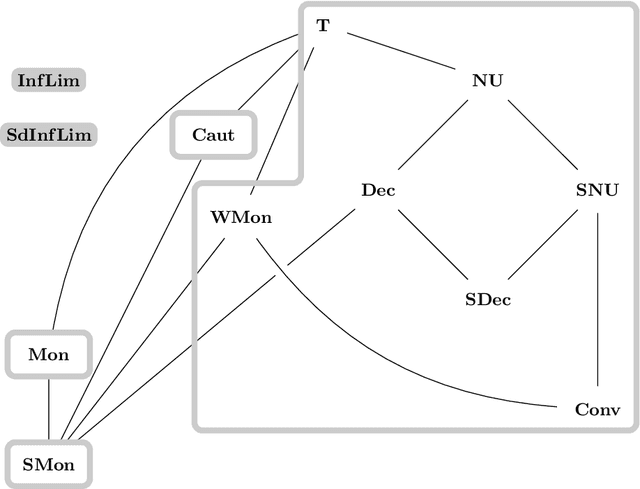
Learning from positive and negative information, so-called \emph{informants}, being one of the models for human and machine learning introduced by Gold, is investigated. Particularly, naturally arising questions about this learning setting, originating in results on learning from solely positive information, are answered. By a carefully arranged argument learners can be assumed to only change their hypothesis in case it is inconsistent with the data (such a learning behavior is called \emph{conservative}). The deduced main theorem states the relations between the most important delayable learning success criteria, being the ones not ruined by a delayed in time hypothesis output. Additionally, our investigations concerning the non-delayable requirement of consistent learning underpin the claim for \emph{delayability} being the right structural property to gain a deeper understanding concerning the nature of learning success criteria. Moreover, we obtain an anomalous \emph{hierarchy} when allowing for an increasing finite number of \emph{anomalies} of the hypothesized language by the learner compared with the language to be learned. In contrast to the vacillatory hierarchy for learning from solely positive information, we observe a \emph{duality} depending on whether infinitely many \emph{vacillations} between different (almost) correct hypotheses are still considered a successful learning behavior.