Learning from Informants: Relations between Learning Success Criteria

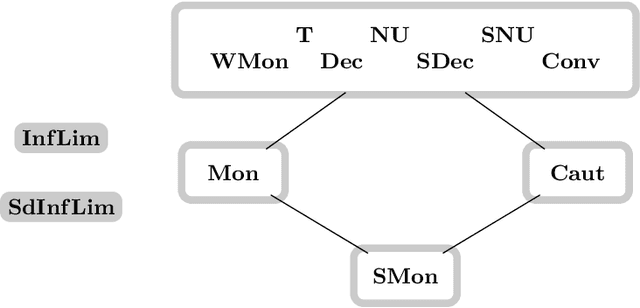
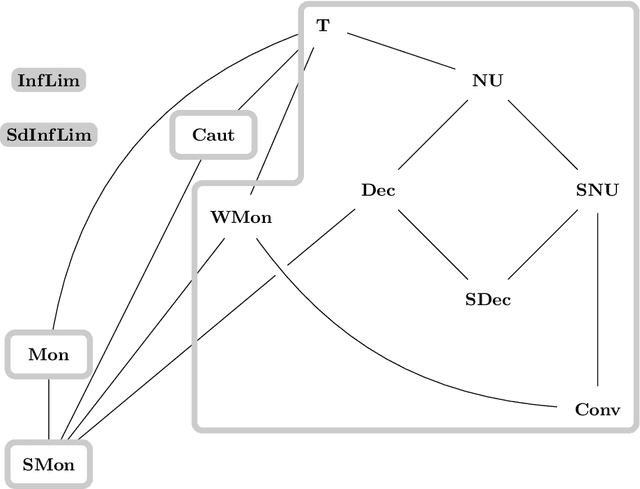
Learning from positive and negative information, so-called \emph{informants}, being one of the models for human and machine learning introduced by Gold, is investigated. Particularly, naturally arising questions about this learning setting, originating in results on learning from solely positive information, are answered. By a carefully arranged argument learners can be assumed to only change their hypothesis in case it is inconsistent with the data (such a learning behavior is called \emph{conservative}). The deduced main theorem states the relations between the most important delayable learning success criteria, being the ones not ruined by a delayed in time hypothesis output. Additionally, our investigations concerning the non-delayable requirement of consistent learning underpin the claim for \emph{delayability} being the right structural property to gain a deeper understanding concerning the nature of learning success criteria. Moreover, we obtain an anomalous \emph{hierarchy} when allowing for an increasing finite number of \emph{anomalies} of the hypothesized language by the learner compared with the language to be learned. In contrast to the vacillatory hierarchy for learning from solely positive information, we observe a \emph{duality} depending on whether infinitely many \emph{vacillations} between different (almost) correct hypotheses are still considered a successful learning behavior.