Learning Languages in the Limit from Positive Information with Finitely Many Memory Changes

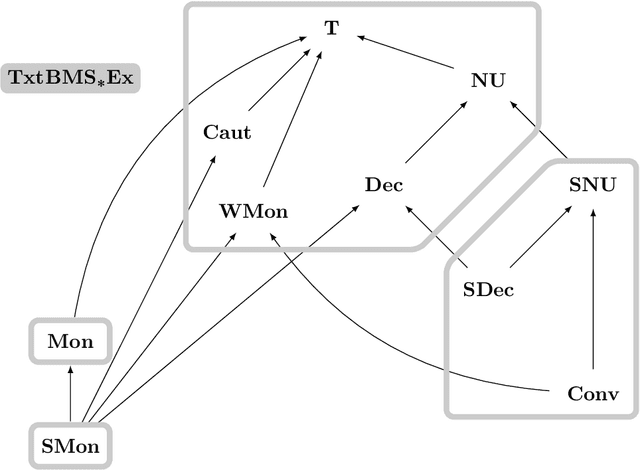
We investigate learning collections of languages from texts by an inductive inference machine with access to the current datum and its memory in form of states. The bounded memory states (BMS) learner is considered successful in case it eventually settles on a correct hypothesis while exploiting only finitely many different states. We give the complete map of all pairwise relations for an established collection of learning success restrictions. Most prominently, we show that non-U-shapedness is not restrictive, while conservativeness and (strong) monotonicity are. Some results carry over from iterative learning by a general lemma showing that, for a wealth of restrictions (the \emph{semantic} restrictions), iterative and bounded memory states learning are equivalent. We also give an example of a non-semantic restriction (strongly non-U-shapedness) where the two settings differ.