Learning Unstable Dynamical Systems with Time-Weighted Logarithmic Loss

When training the parameters of a linear dynamical model, the gradient descent algorithm is likely to fail to converge if the squared-error loss is used as the training loss function. Restricting the parameter space to a smaller subset and running the gradient descent algorithm within this subset can allow learning stable dynamical systems, but this strategy does not work for unstable systems. In this work, we look into the dynamics of the gradient descent algorithm and pinpoint what causes the difficulty of learning unstable systems. We show that observations taken at different times from the system to be learned influence the dynamics of the gradient descent algorithm in substantially different degrees. We introduce a time-weighted logarithmic loss function to fix this imbalance and demonstrate its effectiveness in learning unstable systems.

Persistency of Excitation for Robustness of Neural Networks

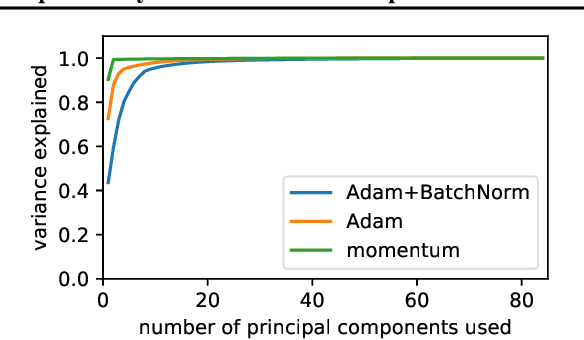
When an online learning algorithm is used to estimate the unknown parameters of a model, the signals interacting with the parameter estimates should not decay too quickly for the optimal values to be discovered correctly. This requirement is referred to as persistency of excitation, and it arises in various contexts, such as optimization with stochastic gradient methods, exploration for multi-armed bandits, and adaptive control of dynamical systems. While training a neural network, the iterative optimization algorithm involved also creates an online learning problem, and consequently, correct estimation of the optimal parameters requires persistent excitation of the network weights. In this work, we analyze the dynamics of the gradient descent algorithm while training a two-layer neural network with two different loss functions, the squared-error loss and the cross-entropy loss; and we obtain conditions to guarantee persistent excitation of the network weights. We then show that these conditions are difficult to satisfy when a multi-layer network is trained for a classification task, for the signals in the intermediate layers of the network become low-dimensional during training and fail to remain persistently exciting. To provide a remedy, we delve into the classical regularization terms used for linear models, reinterpret them as a means to ensure persistent excitation of the model parameters, and propose an algorithm for neural networks by building an analogy. The results in this work shed some light on why adversarial examples have become a challenging problem for neural networks, why merely augmenting training data sets will not be an effective approach to address them, and why there may not exist a data-independent regularization term for neural networks, which involve only the model parameters but not the training data.

Cross-Entropy Loss and Low-Rank Features Have Responsibility for Adversarial Examples

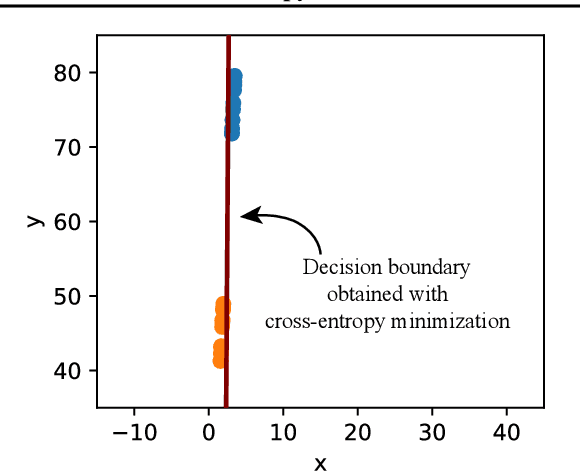
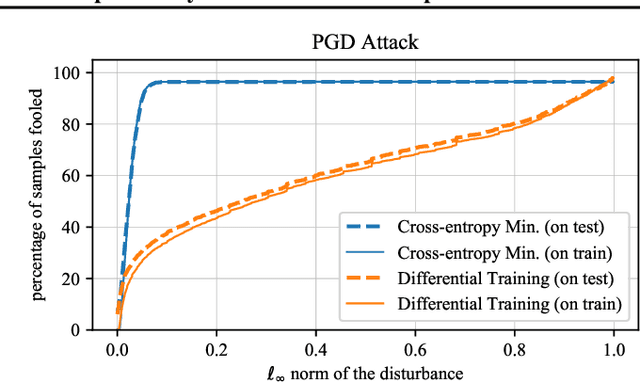
State-of-the-art neural networks are vulnerable to adversarial examples; they can easily misclassify inputs that are imperceptibly different than their training and test data. In this work, we establish that the use of cross-entropy loss function and the low-rank features of the training data have responsibility for the existence of these inputs. Based on this observation, we suggest that addressing adversarial examples requires rethinking the use of cross-entropy loss function and looking for an alternative that is more suited for minimization with low-rank features. In this direction, we present a training scheme called differential training, which uses a loss function defined on the differences between the features of points from opposite classes. We show that differential training can ensure a large margin between the decision boundary of the neural network and the points in the training dataset. This larger margin increases the amount of perturbation needed to flip the prediction of the classifier and makes it harder to find an adversarial example with small perturbations. We test differential training on a binary classification task with CIFAR-10 dataset and demonstrate that it radically reduces the ratio of images for which an adversarial example could be found -- not only in the training dataset, but in the test dataset as well.

Step Size Matters in Deep Learning

Training a neural network with the gradient descent algorithm gives rise to a discrete-time nonlinear dynamical system. Consequently, behaviors that are typically observed in these systems emerge during training, such as convergence to an orbit but not to a fixed point or dependence of convergence on the initialization. Step size of the algorithm plays a critical role in these behaviors: it determines the subset of the local optima that the algorithm can converge to, and it specifies the magnitude of the oscillations if the algorithm converges to an orbit. To elucidate the effects of the step size on training of neural networks, we study the gradient descent algorithm as a discrete-time dynamical system, and by analyzing the Lyapunov stability of different solutions, we show the relationship between the step size of the algorithm and the solutions that can be obtained with this algorithm. The results provide an explanation for several phenomena observed in practice, including the deterioration in the training error with increased depth, the hardness of estimating linear mappings with large singular values, and the distinct performance of deep residual networks.

Residual Networks: Lyapunov Stability and Convex Decomposition

While training error of most deep neural networks degrades as the depth of the network increases, residual networks appear to be an exception. We show that the main reason for this is the Lyapunov stability of the gradient descent algorithm: for an arbitrarily chosen step size, the equilibria of the gradient descent are most likely to remain stable for the parametrization of residual networks. We then present an architecture with a pair of residual networks to approximate a large class of functions by decomposing them into a convex and a concave part. Some parameters of this model are shown to change little during training, and this imperfect optimization prevents overfitting the data and leads to solutions with small Lipschitz constants, while providing clues about the generalization of other deep networks.