High-Dimensional Bayesian Optimization with Manifold Gaussian Processes

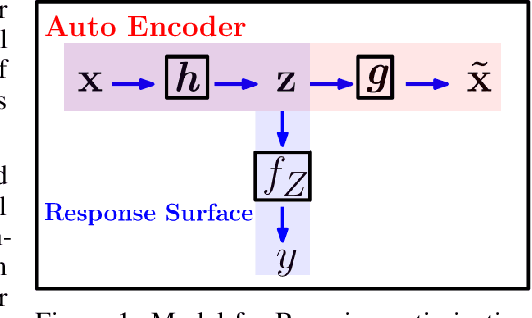
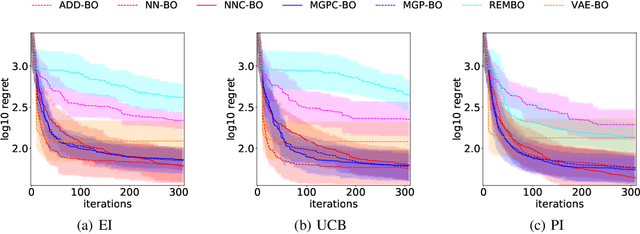
Bayesian optimization (BO) is a powerful approach for seeking the global optimum of expensive black-box functions and has proven successful for fine tuning hyper-parameters of machine learning models. The Bayesian optimization routine involves learning a response surface and maximizing a score to select the most valuable inputs to be queried at the next iteration. These key steps are subject to the curse of dimensionality so that Bayesian optimization does not scale beyond 10--20 parameters. In this work, we address this issue and propose a high-dimensional BO method that learns a nonlinear low-dimensional manifold of the input space. We achieve this with a multi-layer neural network embedded in the covariance function of a Gaussian process. This approach applies unsupervised dimensionality reduction as a byproduct of a supervised regression solution. This also allows exploiting data efficiency of Gaussian process models in a Bayesian framework. We also introduce a nonlinear mapping from the manifold to the high-dimensional space based on multi-output Gaussian processes and jointly train it end-to-end via marginal likelihood maximization. We show this intrinsically low-dimensional optimization outperforms recent baselines in high-dimensional BO literature on a set of benchmark functions in 60 dimensions.

Convex Optimization for Parallel Energy Minimization

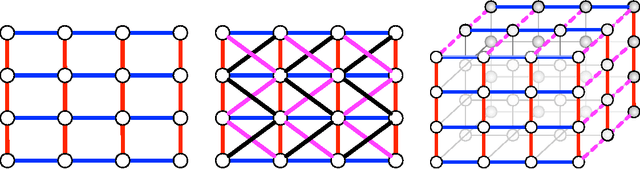
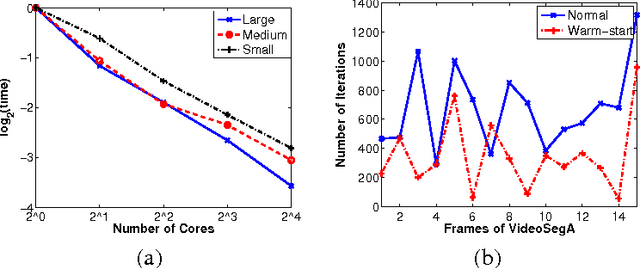
Energy minimization has been an intensely studied core problem in computer vision. With growing image sizes (2D and 3D), it is now highly desirable to run energy minimization algorithms in parallel. But many existing algorithms, in particular, some efficient combinatorial algorithms, are difficult to par-allelize. By exploiting results from convex and submodular theory, we reformulate the quadratic energy minimization problem as a total variation denoising problem, which, when viewed geometrically, enables the use of projection and reflection based convex methods. The resulting min-cut algorithm (and code) is conceptually very simple, and solves a sequence of TV denoising problems. We perform an extensive empirical evaluation comparing state-of-the-art combinatorial algorithms and convex optimization techniques. On small problems the iterative convex methods match the combinatorial max-flow algorithms, while on larger problems they offer other flexibility and important gains: (a) their memory footprint is small; (b) their straightforward parallelizability fits multi-core platforms; (c) they can easily be warm-started; and (d) they quickly reach approximately good solutions, thereby enabling faster "inexact" solutions. A key consequence of our approach based on submodularity and convexity is that it is allows to combine any arbitrary combinatorial or convex methods as subroutines, which allows one to obtain hybrid combinatorial and convex optimization algorithms that benefit from the strengths of both.

Maximizing submodular functions using probabilistic graphical models

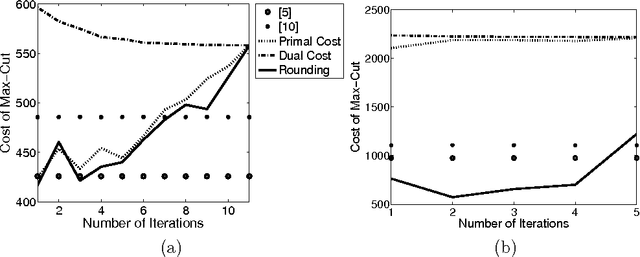
We consider the problem of maximizing submodular functions; while this problem is known to be NP-hard, several numerically efficient local search techniques with approximation guarantees are available. In this paper, we propose a novel convex relaxation which is based on the relationship between submodular functions, entropies and probabilistic graphical models. In a graphical model, the entropy of the joint distribution decomposes as a sum of marginal entropies of subsets of variables; moreover, for any distribution, the entropy of the closest distribution factorizing in the graphical model provides an bound on the entropy. For directed graphical models, this last property turns out to be a direct consequence of the submodularity of the entropy function, and allows the generalization of graphical-model-based upper bounds to any submodular functions. These upper bounds may then be jointly maximized with respect to a set, while minimized with respect to the graph, leading to a convex variational inference scheme for maximizing submodular functions, based on outer approximations of the marginal polytope and maximum likelihood bounded treewidth structures. By considering graphs of increasing treewidths, we may then explore the trade-off between computational complexity and tightness of the relaxation. We also present extensions to constrained problems and maximizing the difference of submodular functions, which include all possible set functions.

Convex Relaxations for Learning Bounded Treewidth Decomposable Graphs

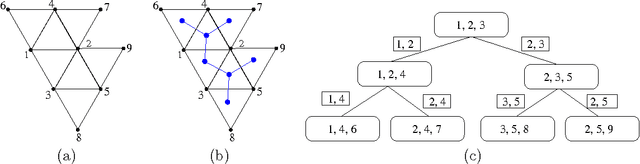
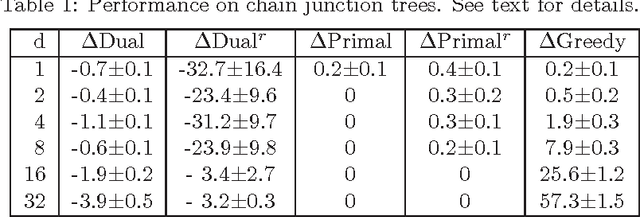
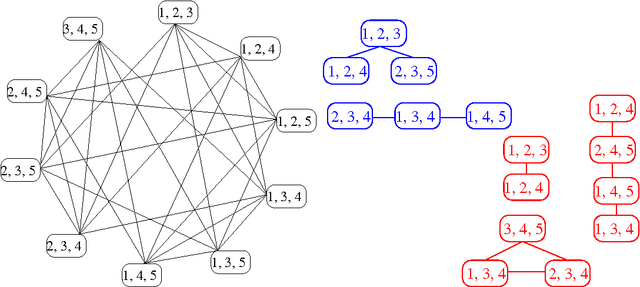
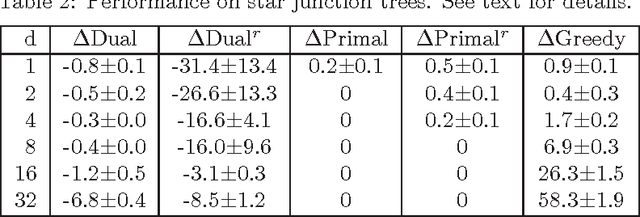
We consider the problem of learning the structure of undirected graphical models with bounded treewidth, within the maximum likelihood framework. This is an NP-hard problem and most approaches consider local search techniques. In this paper, we pose it as a combinatorial optimization problem, which is then relaxed to a convex optimization problem that involves searching over the forest and hyperforest polytopes with special structures, independently. A supergradient method is used to solve the dual problem, with a run-time complexity of $O(k^3 n^{k+2} \log n)$ for each iteration, where $n$ is the number of variables and $k$ is a bound on the treewidth. We compare our approach to state-of-the-art methods on synthetic datasets and classical benchmarks, showing the gains of the novel convex approach.