Convex Relaxations for Learning Bounded Treewidth Decomposable Graphs
Paper and Code
Dec 11, 2012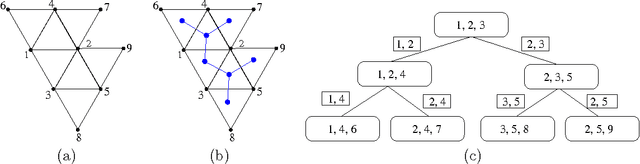
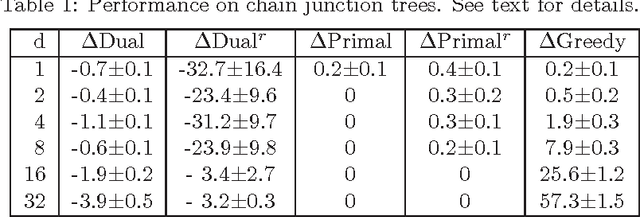
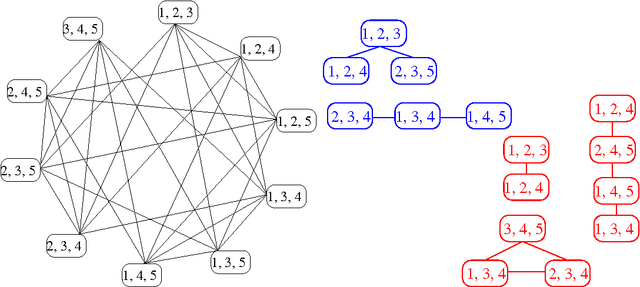
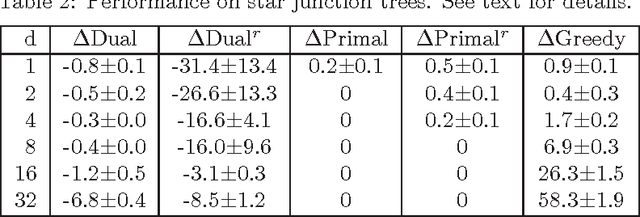
We consider the problem of learning the structure of undirected graphical models with bounded treewidth, within the maximum likelihood framework. This is an NP-hard problem and most approaches consider local search techniques. In this paper, we pose it as a combinatorial optimization problem, which is then relaxed to a convex optimization problem that involves searching over the forest and hyperforest polytopes with special structures, independently. A supergradient method is used to solve the dual problem, with a run-time complexity of $O(k^3 n^{k+2} \log n)$ for each iteration, where $n$ is the number of variables and $k$ is a bound on the treewidth. We compare our approach to state-of-the-art methods on synthetic datasets and classical benchmarks, showing the gains of the novel convex approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge