Submodular Maximization Beyond Non-negativity: Guarantees, Fast Algorithms, and Applications

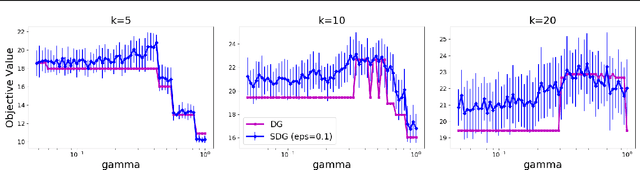
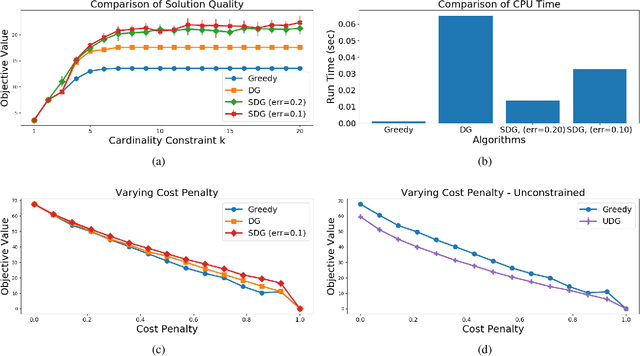
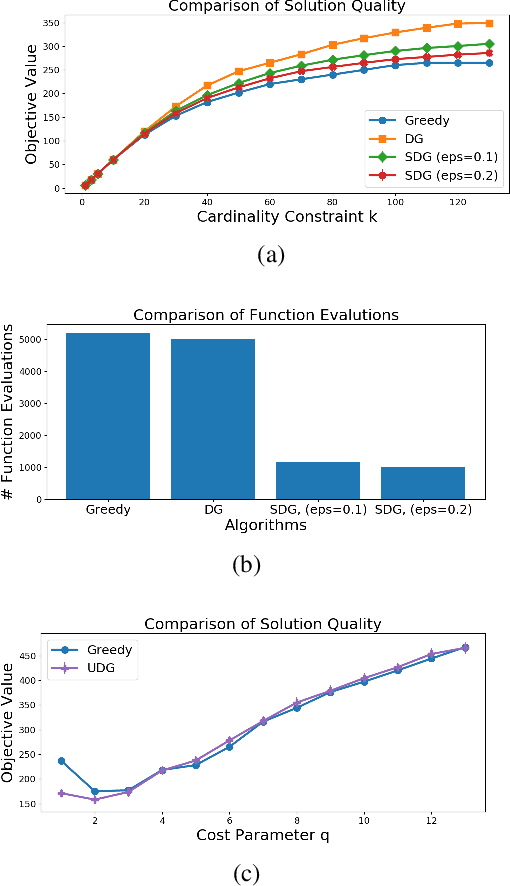
It is generally believed that submodular functions -- and the more general class of $\gamma$-weakly submodular functions -- may only be optimized under the non-negativity assumption $f(S) \geq 0$. In this paper, we show that once the function is expressed as the difference $f = g - c$, where $g$ is monotone, non-negative, and $\gamma$-weakly submodular and $c$ is non-negative modular, then strong approximation guarantees may be obtained. We present an algorithm for maximizing $g - c$ under a $k$-cardinality constraint which produces a random feasible set $S$ such that $\mathbb{E} \left[ g(S) - c(S) \right] \geq (1 - e^{-\gamma} - \epsilon) g(OPT) - c(OPT)$, whose running time is $O (\frac{n}{\epsilon} \log^2 \frac{1}{\epsilon})$, i.e., independent of $k$. We extend these results to the unconstrained setting by describing an algorithm with the same approximation guarantees and faster $O(\frac{n}{\epsilon} \log\frac{1}{\epsilon})$ runtime. The main techniques underlying our algorithms are two-fold: the use of a surrogate objective which varies the relative importance between $g$ and $c$ throughout the algorithm, and a geometric sweep over possible $\gamma$ values. Our algorithmic guarantees are complemented by a hardness result showing that no polynomial-time algorithm which accesses $g$ through a value oracle can do better. We empirically demonstrate the success of our algorithms by applying them to experimental design on the Boston Housing dataset and directed vertex cover on the Email EU dataset.

A New Framework for Distributed Submodular Maximization

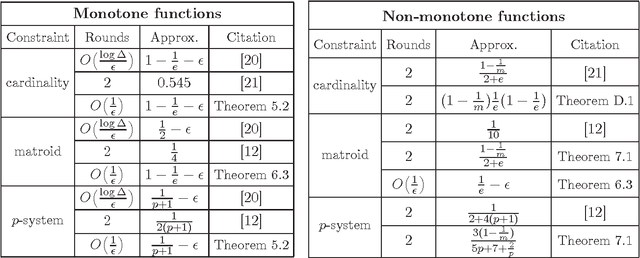
A wide variety of problems in machine learning, including exemplar clustering, document summarization, and sensor placement, can be cast as constrained submodular maximization problems. A lot of recent effort has been devoted to developing distributed algorithms for these problems. However, these results suffer from high number of rounds, suboptimal approximation ratios, or both. We develop a framework for bringing existing algorithms in the sequential setting to the distributed setting, achieving near optimal approximation ratios for many settings in only a constant number of MapReduce rounds. Our techniques also give a fast sequential algorithm for non-monotone maximization subject to a matroid constraint.

The Power of Randomization: Distributed Submodular Maximization on Massive Datasets

A wide variety of problems in machine learning, including exemplar clustering, document summarization, and sensor placement, can be cast as constrained submodular maximization problems. Unfortunately, the resulting submodular optimization problems are often too large to be solved on a single machine. We develop a simple distributed algorithm that is embarrassingly parallel and it achieves provable, constant factor, worst-case approximation guarantees. In our experiments, we demonstrate its efficiency in large problems with different kinds of constraints with objective values always close to what is achievable in the centralized setting.