Semi-Supervised Hyperbolic Hierarchical Clustering with Set-Level Structural Priors

Semi-supervised hierarchical clustering aims to learn a tree structure consistent with data patterns and user-provided supervision. Supervision is usually given as leaf-level relations, such as pairwise must-link/cannot-link constraints or triplet-wise must-link-before constraints. Although useful for regulating local sample relations, such supervision does not directly indicate which samples should form coherent subtrees. Consequently, the non-leaf structure of the learned tree may deviate from the hierarchical organization preferred by ground-truth labels. To address this limitation, we propose a semi-supervised hyperbolic hierarchical clustering method with set-level structural priors. The main contribution is to introduce sets as basic modeling units for hierarchy learning. Each set denotes samples expected to cohere within a subtree and is induced from leaf-level supervision together with a learned constraint-consistent similarity structure. These sets act as soft structural priors for subtree-level supervision, allowing supervision to guide non-leaf hierarchy formation beyond local leaf-level relations. Specifically, we first learn constraint-consistent embeddings to obtain a reliable set partition, then construct constraint-induced sets and estimate inter-set similarities to form set-level structural priors. Finally, these priors are incorporated into a hyperbolic hierarchy objective for continuous tree optimization. Experiments on eleven benchmark datasets and ablation studies show that the proposed method consistently improves label consistency over representative hierarchical clustering baselines while also enhancing similarity-based tree quality.

Sparse Tensor PCA via Tensor Decomposition for Unsupervised Feature Selection

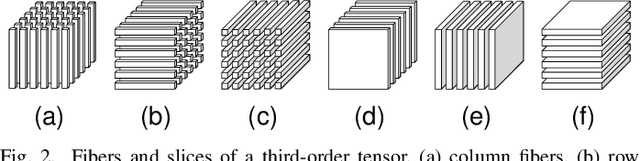
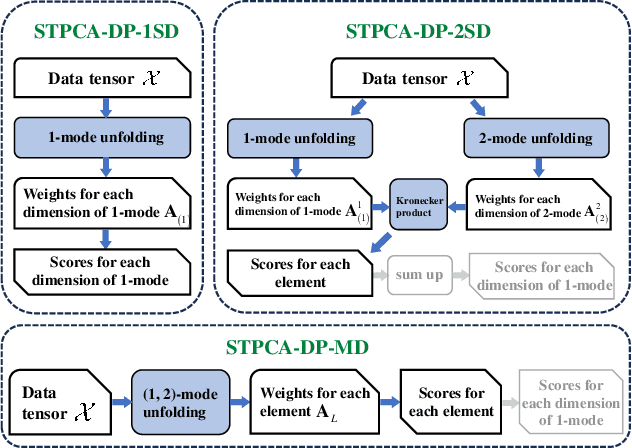
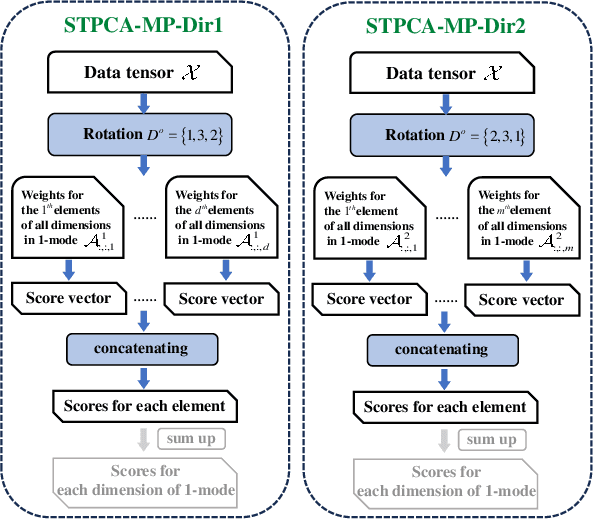
Recently, introducing Tensor Decomposition (TD) methods into unsupervised feature selection (UFS) has been a rising research point. A tensor structure is beneficial for mining the relations between different modes and helps relieve the computation burden. However, while existing methods exploit TD to minimize the reconstruction error of a data tensor, they don't fully utilize the interpretable and discriminative information in the factor matrices. Moreover, most methods require domain knowledge to perform feature selection. To solve the above problems, we develop two Sparse Tensor Principal Component Analysis (STPCA) models that utilize the projection directions in the factor matrices to perform UFS. The first model extends Tucker Decomposition to a multiview sparse regression form and is transformed into several alternatively solved convex subproblems. The second model formulates a sparse version of the family of Tensor Singular Value Decomposition (T-SVDs) and is transformed into individual convex subproblems. For both models, we prove the optimal solution of each subproblem falls onto the Hermitian Positive Semidefinite Cone (HPSD). Accordingly, we design two fast algorithms based on HPSD projection and prove their convergence. According to the experimental results on two original synthetic datasets (Orbit and Array Signal) and five real-world datasets, the two proposed methods are suitable for handling different data tensor scenarios and outperform the state-of-the-art UFS methods.

Fast Sparse PCA via Positive Semidefinite Projection for Unsupervised Feature Selection

In the field of unsupervised feature selection, sparse principal component analysis (SPCA) methods have attracted more and more attention recently. Compared to spectral-based methods, SPCA methods don't rely on the construction of a similarity matrix and show better feature selection ability on real-world data. The original SPCA formulates a nonconvex optimization problem. Existing convex SPCA methods reformulate SPCA as a convex model by regarding the reconstruction matrix as an optimization variable. However, they are lack of constraints equivalent to the orthogonality restriction in SPCA, leading to larger solution space. In this paper, it's proved that the optimal solution to a convex SPCA model falls onto the Positive Semidefinite (PSD) cone. A standard convex SPCA-based model with PSD constraint for unsupervised feature selection is proposed. Further, a two-step fast optimization algorithm via PSD projection is presented to solve the proposed model. Two other existing convex SPCA-based models are also proven to have their solutions optimized on the PSD cone in this paper. Therefore, the PSD versions of these two models are proposed to accelerate their convergence as well. We also provide a regularization parameter setting strategy for our proposed method. Experiments on synthetic and real-world datasets demonstrate the effectiveness and efficiency of the proposed methods.