Julien M. Hendrickx
Physics-informed data-driven control without persistence of excitation
Apr 11, 2025Abstract:We show that data that is not sufficiently informative to allow for system re-identification can still provide meaningful information when combined with external or physical knowledge of the system, such as bounded system matrix norms. We then illustrate how this information can be leveraged for safety and energy minimization problems and to enhance predictions in unmodelled dynamics. This preliminary work outlines key ideas toward using limited data for effective control by integrating physical knowledge of the system and exploiting interpolation conditions.
2-D Directed Formation Control Based on Bipolar Coordinates
Aug 02, 2021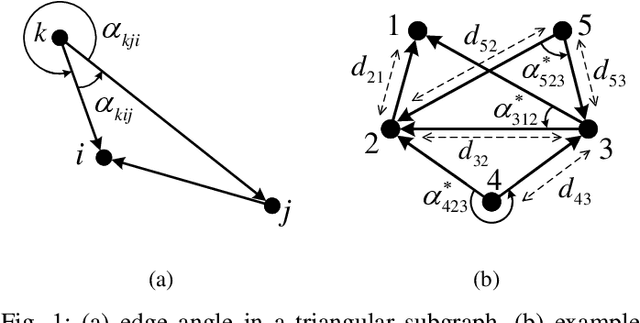
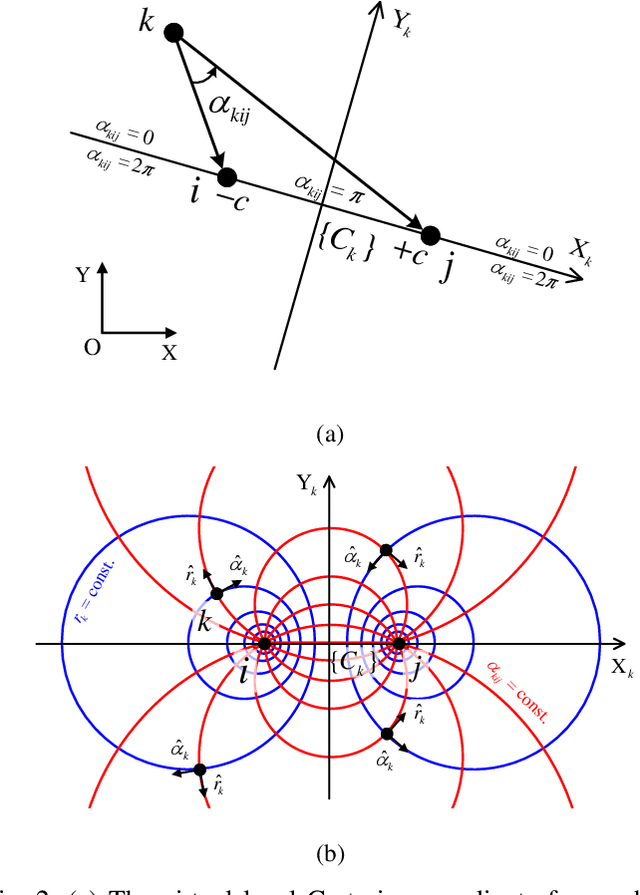
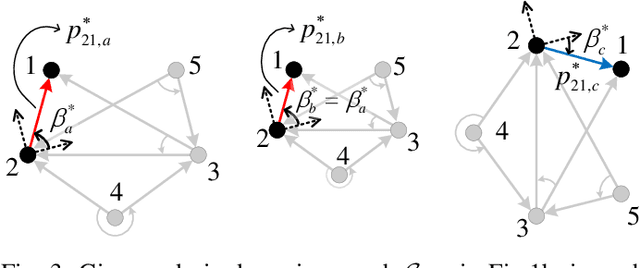
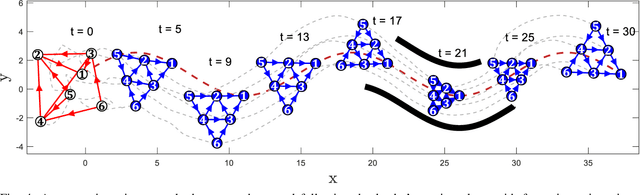
Abstract:This work proposes a novel 2-D formation control scheme for acyclic triangulated directed graphs (a class of minimally acyclic persistent graphs) based on bipolar coordinates with (almost) global convergence to the desired shape. Prescribed performance control is employed to devise a decentralized control law that avoids singularities and introduces robustness against external disturbances while ensuring predefined transient and steady-state performance for the closed-loop system. Furthermore, it is shown that the proposed formation control scheme can handle formation maneuvering, scaling, and orientation specifications simultaneously. Additionally, the proposed control law is implementable in the agents' arbitrarily oriented local coordinate frames using only low-cost onboard vision sensors, which are favorable for practical applications. Finally, various simulation studies clarify and verify the proposed approach.
Graph Resistance and Learning from Pairwise Comparisons
Feb 01, 2019
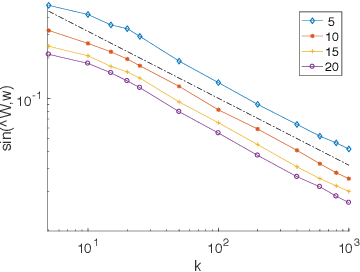
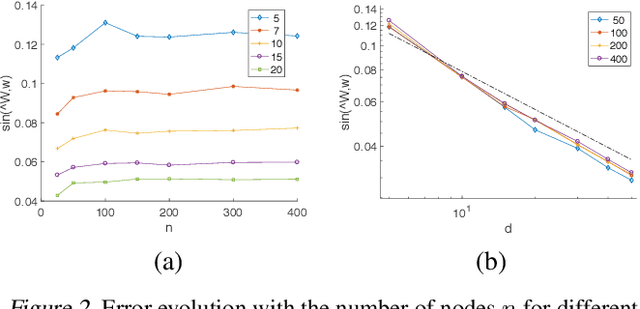
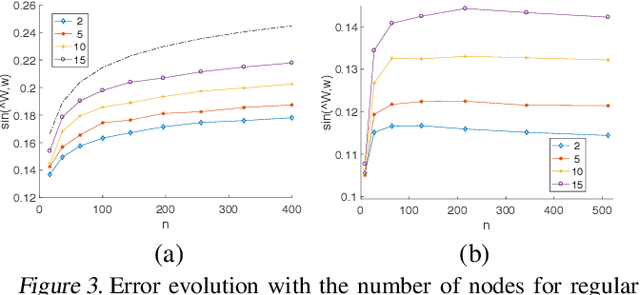
Abstract:We consider the problem of learning the qualities of a collection of items by performing noisy comparisons among them. Following the standard paradigm, we assume there is a fixed "comparison graph" and every neighboring pair of items in this graph is compared $k$ times according to the Bradley-Terry-Luce model (where the probability than an item wins a comparison is proportional the item quality). We are interested in how the relative error in quality estimation scales with the comparison graph in the regime where $k$ is large. We prove that, after a known transition period, the relevant graph-theoretic quantity is the square root of the resistance of the comparison graph. Specifically, we provide an algorithm that is minimax optimal. The algorithm has a relative error decay that scales with the square root of the graph resistance, and provide a matching lower bound (up to log factors). The performance guarantee of our algorithm, both in terms of the graph and the skewness of the item quality distribution, outperforms earlier results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge