Graph Resistance and Learning from Pairwise Comparisons
Paper and Code
Feb 01, 2019
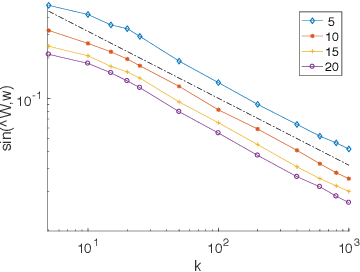
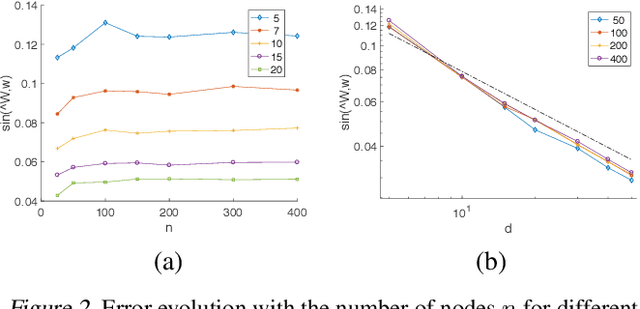
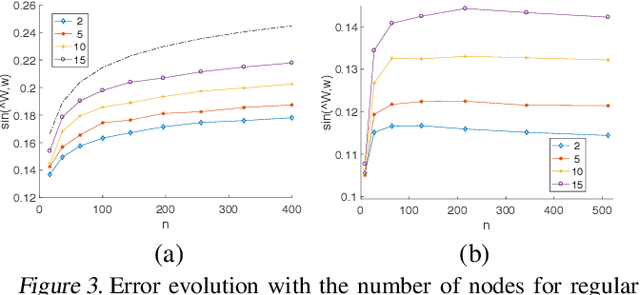
We consider the problem of learning the qualities of a collection of items by performing noisy comparisons among them. Following the standard paradigm, we assume there is a fixed "comparison graph" and every neighboring pair of items in this graph is compared $k$ times according to the Bradley-Terry-Luce model (where the probability than an item wins a comparison is proportional the item quality). We are interested in how the relative error in quality estimation scales with the comparison graph in the regime where $k$ is large. We prove that, after a known transition period, the relevant graph-theoretic quantity is the square root of the resistance of the comparison graph. Specifically, we provide an algorithm that is minimax optimal. The algorithm has a relative error decay that scales with the square root of the graph resistance, and provide a matching lower bound (up to log factors). The performance guarantee of our algorithm, both in terms of the graph and the skewness of the item quality distribution, outperforms earlier results.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge