Julien Corman
Complete Approximations of Incomplete Queries
Jul 30, 2024Abstract:This paper studies the completeness of conjunctive queries over a partially complete database and the approximation of incomplete queries. Given a query and a set of completeness rules (a special kind of tuple generating dependencies) that specify which parts of the database are complete, we investigate whether the query can be fully answered, as if all data were available. If not, we explore reformulating the query into either Maximal Complete Specializations (MCSs) or the (unique up to equivalence) Minimal Complete Generalization (MCG) that can be fully answered, that is, the best complete approximations of the query from below or above in the sense of query containment. We show that the MSG can be characterized as the least fixed-point of a monotonic operator in a preorder. Then, we show that an MCS can be computed by recursive backward application of completeness rules. We study the complexity of both problems and discuss implementation techniques that rely on an ASP and Prolog engines, respectively.
Counting Query Answers over a DL-Lite Knowledge Base
May 25, 2020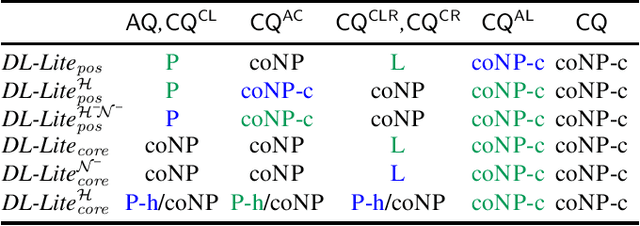
Abstract:Counting answers to a query is an operation supported by virtually all database management systems. In this paper we focus on counting answers over a Knowledge Base (KB), which may be viewed as a database enriched with background knowledge about the domain under consideration. In particular, we place our work in the context of Ontology-Mediated Query Answering/Ontology-based Data Access (OMQA/OBDA), where the language used for the ontology is a member of the DL-Lite family and the data is a (usually virtual) set of assertions. We study the data complexity of query answering, for different members of the DL-Lite family that include number restrictions, and for variants of conjunctive queries with counting that differ with respect to their shape (connected, branching, rooted). We improve upon existing results by providing a PTIME and coNP lower bounds, and upper bounds in PTIME and LOGSPACE. For the latter case, we define a novel query rewriting technique into first-order logic with counting.
Certain Answers to a SPARQL Query over a Knowledge Base
Nov 21, 2019
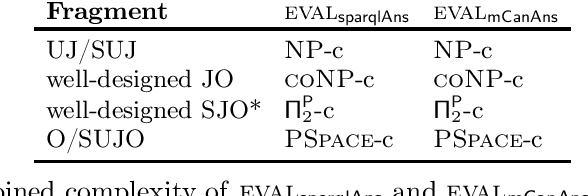
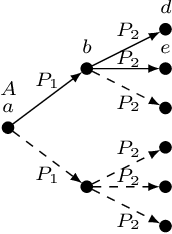
Abstract:Ontology-Mediated Query Answering (OMQA) is a well-established framework to answer queries over an RDFS or OWL Knowledge Base (KB). OMQA was originally designed for unions of conjunctive queries (UCQs), and based on certain answers. More recently, OMQA has been extended to SPARQL queries, but to our knowledge, none of the efforts made in this direction (either in the literature, or the so-called SPARQL entailment regimes) is able to capture both certain answers for UCQs and the standard interpretation of SPARQL over a plain graph. We formalize these as requirements to be met by any semantics aiming at conciliating certain answers and SPARQL answers, and define three additional requirements, which generalize to KBs some basic properties of SPARQL answers. Then we show that a semantics can be defined that satisfies all requirements for SPARQL queries with SELECT, UNION, and OPTIONAL, and for DLs with the canonical model property. We also investigate combined complexity for query answering under such a semantics over DL-Lite R KBs. In particular, we show for different fragments of SPARQL that known upper-bounds for query answering over a plain graph are matched.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge