Julian Bitterwolf
In or Out? Fixing ImageNet Out-of-Distribution Detection Evaluation
Jun 01, 2023



Abstract:Out-of-distribution (OOD) detection is the problem of identifying inputs which are unrelated to the in-distribution task. The OOD detection performance when the in-distribution (ID) is ImageNet-1K is commonly being tested on a small range of test OOD datasets. We find that most of the currently used test OOD datasets, including datasets from the open set recognition (OSR) literature, have severe issues: In some cases more than 50$\%$ of the dataset contains objects belonging to one of the ID classes. These erroneous samples heavily distort the evaluation of OOD detectors. As a solution, we introduce with NINCO a novel test OOD dataset, each sample checked to be ID free, which with its fine-grained range of OOD classes allows for a detailed analysis of an OOD detector's strengths and failure modes, particularly when paired with a number of synthetic "OOD unit-tests". We provide detailed evaluations across a large set of architectures and OOD detection methods on NINCO and the unit-tests, revealing new insights about model weaknesses and the effects of pretraining on OOD detection performance. We provide code and data at https://github.com/j-cb/NINCO.
Breaking Down Out-of-Distribution Detection: Many Methods Based on OOD Training Data Estimate a Combination of the Same Core Quantities
Jun 20, 2022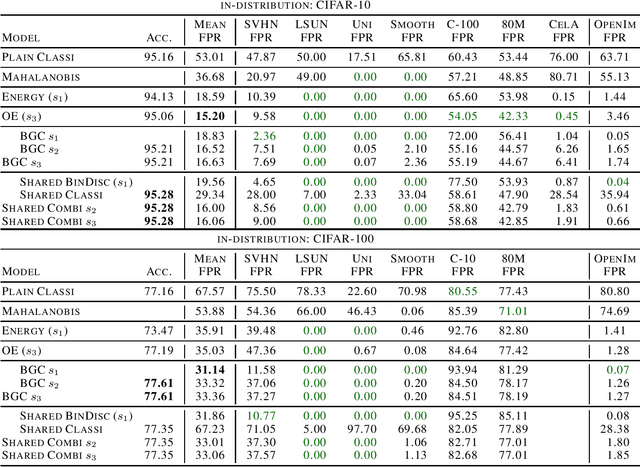
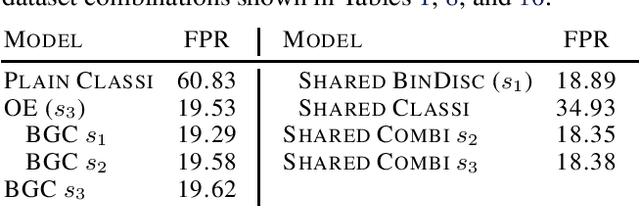
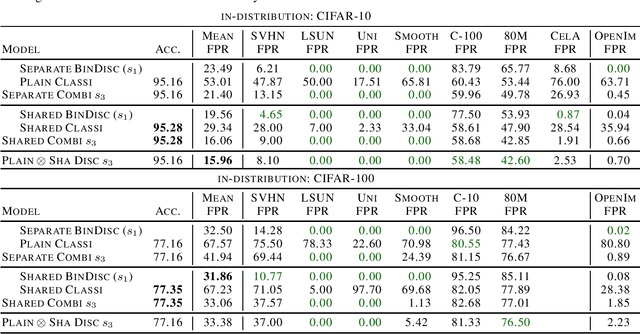

Abstract:It is an important problem in trustworthy machine learning to recognize out-of-distribution (OOD) inputs which are inputs unrelated to the in-distribution task. Many out-of-distribution detection methods have been suggested in recent years. The goal of this paper is to recognize common objectives as well as to identify the implicit scoring functions of different OOD detection methods. We focus on the sub-class of methods that use surrogate OOD data during training in order to learn an OOD detection score that generalizes to new unseen out-distributions at test time. We show that binary discrimination between in- and (different) out-distributions is equivalent to several distinct formulations of the OOD detection problem. When trained in a shared fashion with a standard classifier, this binary discriminator reaches an OOD detection performance similar to that of Outlier Exposure. Moreover, we show that the confidence loss which is used by Outlier Exposure has an implicit scoring function which differs in a non-trivial fashion from the theoretically optimal scoring function in the case where training and test out-distribution are the same, which again is similar to the one used when training an Energy-Based OOD detector or when adding a background class. In practice, when trained in exactly the same way, all these methods perform similarly.
Provably Robust Detection of Out-of-distribution Data (almost) for free
Jun 08, 2021
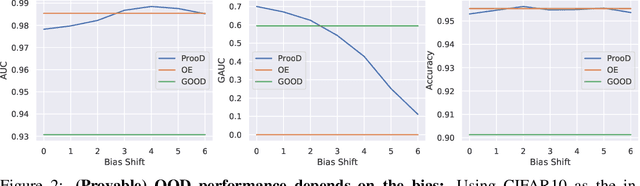
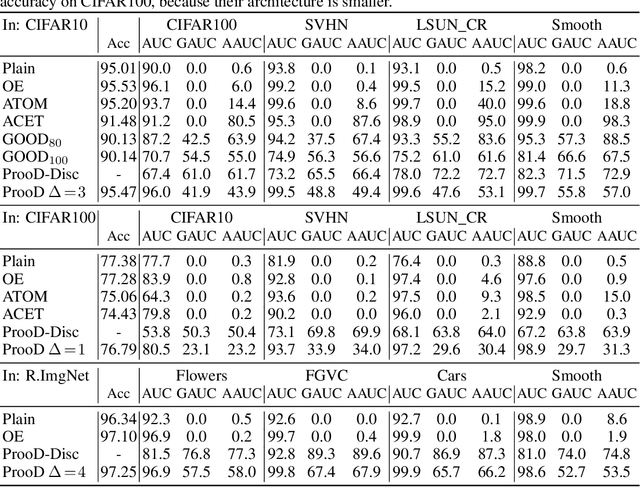
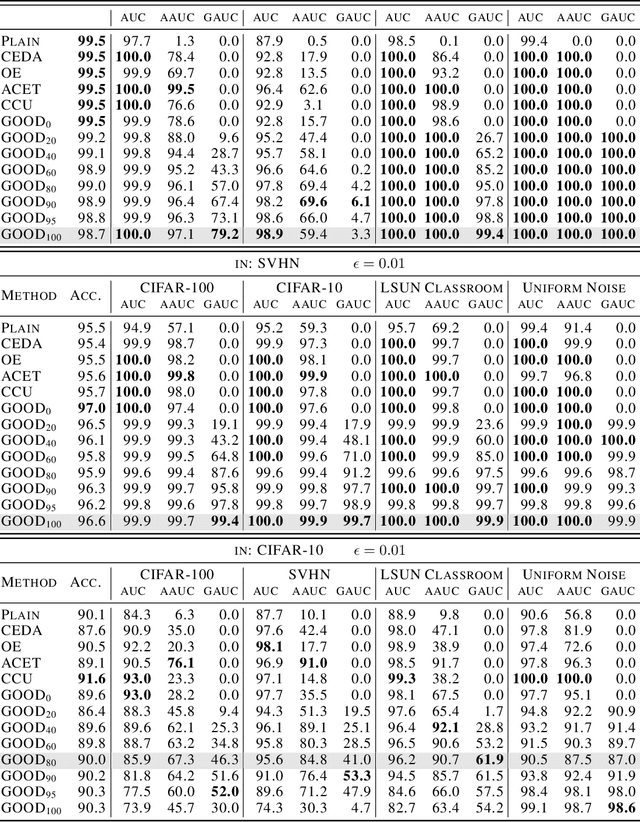
Abstract:When applying machine learning in safety-critical systems, a reliable assessment of the uncertainy of a classifier is required. However, deep neural networks are known to produce highly overconfident predictions on out-of-distribution (OOD) data and even if trained to be non-confident on OOD data one can still adversarially manipulate OOD data so that the classifer again assigns high confidence to the manipulated samples. In this paper we propose a novel method where from first principles we combine a certifiable OOD detector with a standard classifier into an OOD aware classifier. In this way we achieve the best of two worlds: certifiably adversarially robust OOD detection, even for OOD samples close to the in-distribution, without loss in prediction accuracy and close to state-of-the-art OOD detection performance for non-manipulated OOD data. Moreover, due to the particular construction our classifier provably avoids the asymptotic overconfidence problem of standard neural networks.
Provable Worst Case Guarantees for the Detection of Out-of-Distribution Data
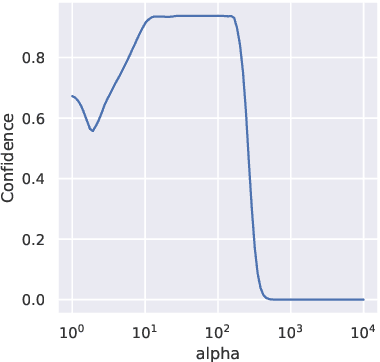
Jul 16, 2020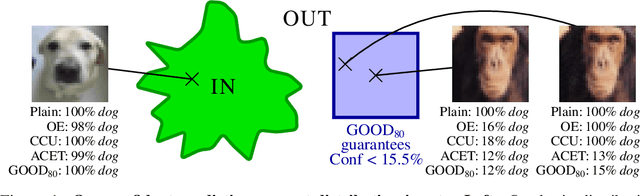

Abstract:Deep neural networks are known to be overconfident when applied to out-of-distribution (OOD) inputs which clearly do not belong to any class. This is a problem in safety-critical applications since a reliable assessment of the uncertainty of a classifier is a key property, allowing to trigger human intervention or to transfer into a safe state. In this paper, we are aiming for certifiable worst case guarantees for OOD detection by enforcing not only low confidence at the OOD point but also in an $l_\infty$-ball around it. For this purpose, we use interval bound propagation (IBP) to upper bound the maximal confidence in the $l_\infty$-ball and minimize this upper bound during training time. We show that non-trivial bounds on the confidence for OOD data generalizing beyond the OOD dataset seen at training time are possible. Moreover, in contrast to certified adversarial robustness which typically comes with significant loss in prediction performance, certified guarantees for worst case OOD detection are possible without much loss in accuracy.
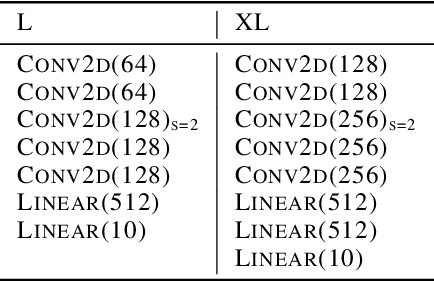
Increasing the robustness of DNNs against image corruptions by playing the Game of Noise
Feb 26, 2020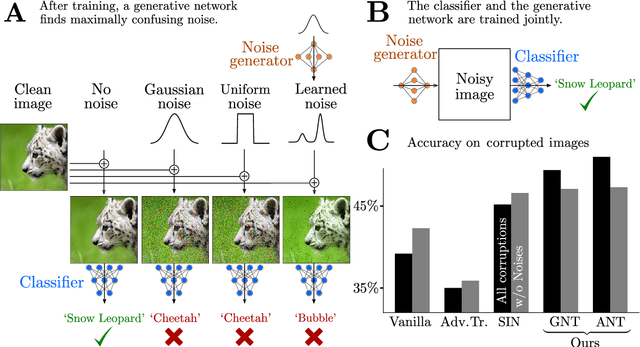
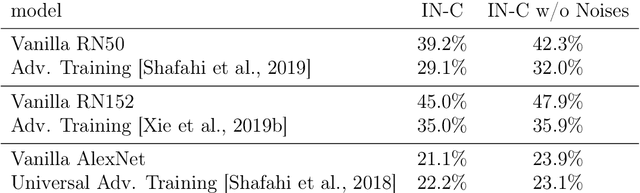
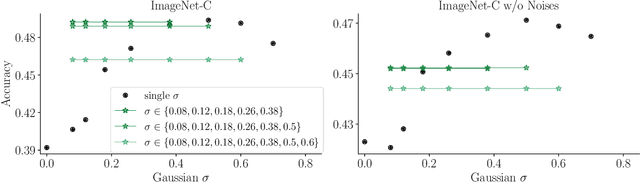
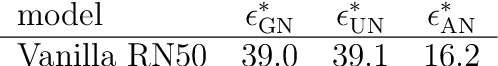
Abstract:The human visual system is remarkably robust against a wide range of naturally occurring variations and corruptions like rain or snow. In contrast, the performance of modern image recognition models strongly degrades when evaluated on previously unseen corruptions. Here, we demonstrate that a simple but properly tuned training with additive Gaussian and Speckle noise generalizes surprisingly well to unseen corruptions, easily reaching the previous state of the art on the corruption benchmark ImageNet-C (with ResNet50) and on MNIST-C. We build on top of these strong baseline results and show that an adversarial training of the recognition model against uncorrelated worst-case noise distributions leads to an additional increase in performance. This regularization can be combined with previously proposed defense methods for further improvement.
Why ReLU networks yield high-confidence predictions far away from the training data and how to mitigate the problem
Dec 13, 2018
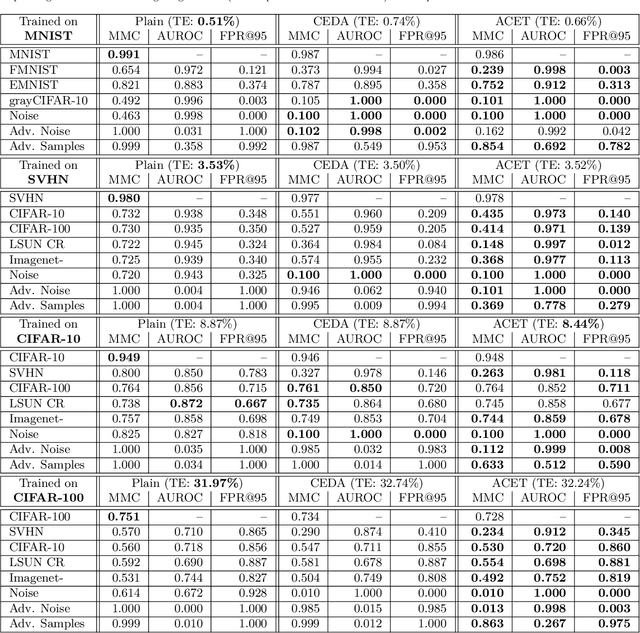


Abstract:Classifiers used in the wild, in particular for safety-critical systems, should not only have good generalization properties but also should know when they don't know, in particular make low confidence predictions far away from the training data. We show that ReLU type neural networks which yield a piecewise linear classifier function fail in this regard as they produce almost always high confidence predictions far away from the training data. For bounded domains like images we propose a new robust optimization technique similar to adversarial training which enforces low confidence predictions far away from the training data. We show that this technique is surprisingly effective in reducing the confidence of predictions far away from the training data while maintaining high confidence predictions and similar test error on the original classification task compared to standard training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge