Breaking Down Out-of-Distribution Detection: Many Methods Based on OOD Training Data Estimate a Combination of the Same Core Quantities
Paper and Code
Jun 20, 2022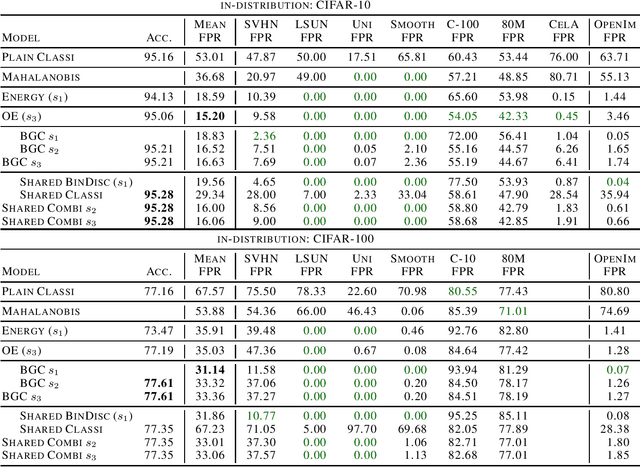
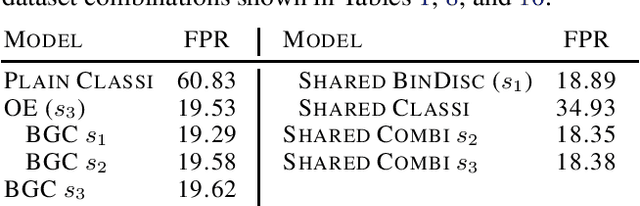
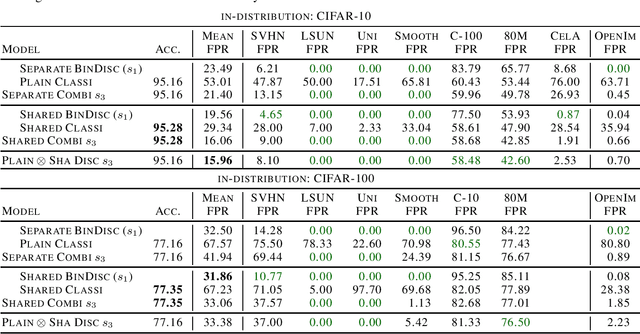

It is an important problem in trustworthy machine learning to recognize out-of-distribution (OOD) inputs which are inputs unrelated to the in-distribution task. Many out-of-distribution detection methods have been suggested in recent years. The goal of this paper is to recognize common objectives as well as to identify the implicit scoring functions of different OOD detection methods. We focus on the sub-class of methods that use surrogate OOD data during training in order to learn an OOD detection score that generalizes to new unseen out-distributions at test time. We show that binary discrimination between in- and (different) out-distributions is equivalent to several distinct formulations of the OOD detection problem. When trained in a shared fashion with a standard classifier, this binary discriminator reaches an OOD detection performance similar to that of Outlier Exposure. Moreover, we show that the confidence loss which is used by Outlier Exposure has an implicit scoring function which differs in a non-trivial fashion from the theoretically optimal scoring function in the case where training and test out-distribution are the same, which again is similar to the one used when training an Energy-Based OOD detector or when adding a background class. In practice, when trained in exactly the same way, all these methods perform similarly.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge