Effective LHC measurements with matrix elements and machine learning

One major challenge for the legacy measurements at the LHC is that the likelihood function is not tractable when the collected data is high-dimensional and the detector response has to be modeled. We review how different analysis strategies solve this issue, including the traditional histogram approach used in most particle physics analyses, the Matrix Element Method, Optimal Observables, and modern techniques based on neural density estimation. We then discuss powerful new inference methods that use a combination of matrix element information and machine learning to accurately estimate the likelihood function. The MadMiner package automates all necessary data-processing steps. In first studies we find that these new techniques have the potential to substantially improve the sensitivity of the LHC legacy measurements.

Mining gold from implicit models to improve likelihood-free inference

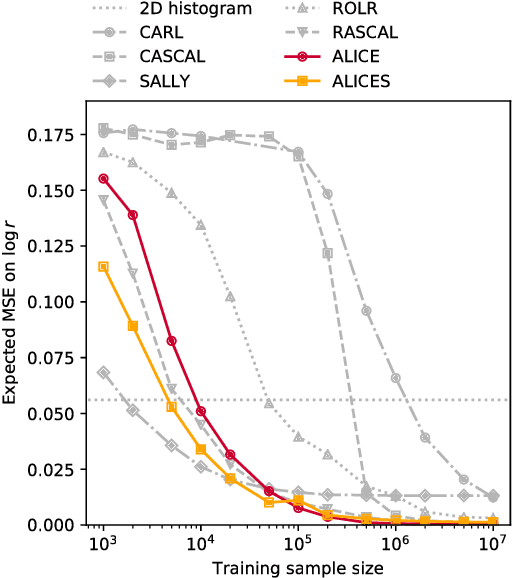
Simulators often provide the best description of real-world phenomena. However, they also lead to challenging inverse problems because the density they implicitly define is often intractable. We present a new suite of simulation-based inference techniques that go beyond the traditional Approximate Bayesian Computation approach, which struggles in a high-dimensional setting, and extend methods that use surrogate models based on neural networks. We show that additional information, such as the joint likelihood ratio and the joint score, can often be extracted from simulators and used to augment the training data for these surrogate models. Finally, we demonstrate that these new techniques are more sample efficient and provide higher-fidelity inference than traditional methods.

Likelihood-free inference with an improved cross-entropy estimator

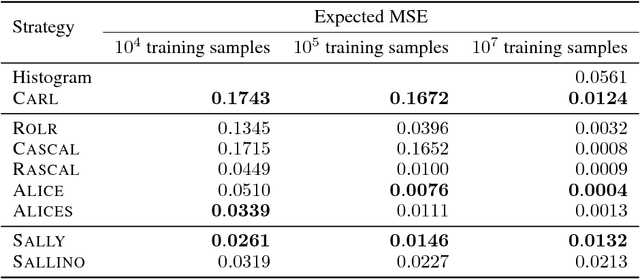
We extend recent work (Brehmer, et. al., 2018) that use neural networks as surrogate models for likelihood-free inference. As in the previous work, we exploit the fact that the joint likelihood ratio and joint score, conditioned on both observed and latent variables, can often be extracted from an implicit generative model or simulator to augment the training data for these surrogate models. We show how this augmented training data can be used to provide a new cross-entropy estimator, which provides improved sample efficiency compared to previous loss functions exploiting this augmented training data.

A Guide to Constraining Effective Field Theories with Machine Learning

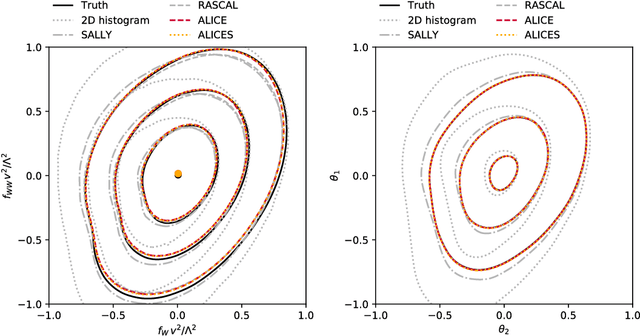
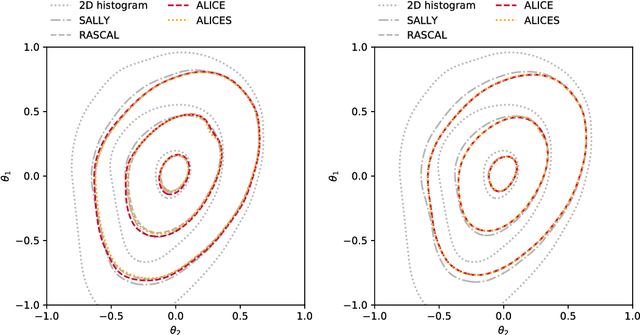
We develop, discuss, and compare several inference techniques to constrain theory parameters in collider experiments. By harnessing the latent-space structure of particle physics processes, we extract extra information from the simulator. This augmented data can be used to train neural networks that precisely estimate the likelihood ratio. The new methods scale well to many observables and high-dimensional parameter spaces, do not require any approximations of the parton shower and detector response, and can be evaluated in microseconds. Using weak-boson-fusion Higgs production as an example process, we compare the performance of several techniques. The best results are found for likelihood ratio estimators trained with extra information about the score, the gradient of the log likelihood function with respect to the theory parameters. The score also provides sufficient statistics that contain all the information needed for inference in the neighborhood of the Standard Model. These methods enable us to put significantly stronger bounds on effective dimension-six operators than the traditional approach based on histograms. They also outperform generic machine learning methods that do not make use of the particle physics structure, demonstrating their potential to substantially improve the new physics reach of the LHC legacy results.

Constraining Effective Field Theories with Machine Learning

We present powerful new analysis techniques to constrain effective field theories at the LHC. By leveraging the structure of particle physics processes, we extract extra information from Monte-Carlo simulations, which can be used to train neural network models that estimate the likelihood ratio. These methods scale well to processes with many observables and theory parameters, do not require any approximations of the parton shower or detector response, and can be evaluated in microseconds. We show that they allow us to put significantly stronger bounds on dimension-six operators than existing methods, demonstrating their potential to improve the precision of the LHC legacy constraints.

Working Memory Networks: Augmenting Memory Networks with a Relational Reasoning Module

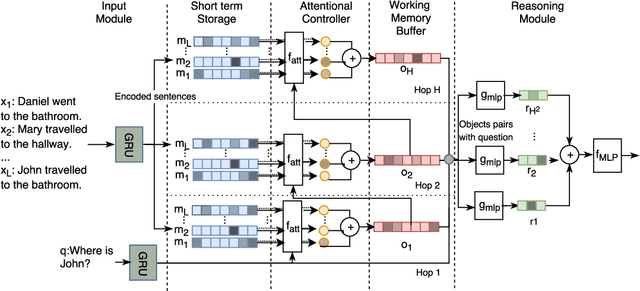
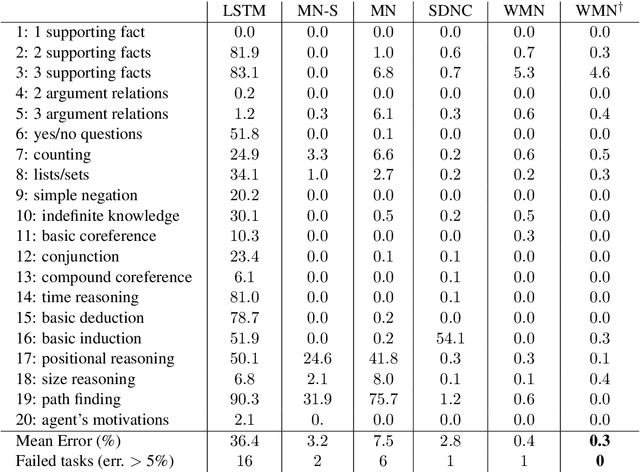
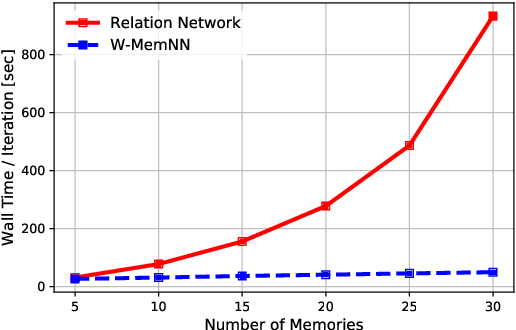
During the last years, there has been a lot of interest in achieving some kind of complex reasoning using deep neural networks. To do that, models like Memory Networks (MemNNs) have combined external memory storages and attention mechanisms. These architectures, however, lack of more complex reasoning mechanisms that could allow, for instance, relational reasoning. Relation Networks (RNs), on the other hand, have shown outstanding results in relational reasoning tasks. Unfortunately, their computational cost grows quadratically with the number of memories, something prohibitive for larger problems. To solve these issues, we introduce the Working Memory Network, a MemNN architecture with a novel working memory storage and reasoning module. Our model retains the relational reasoning abilities of the RN while reducing its computational complexity from quadratic to linear. We tested our model on the text QA dataset bAbI and the visual QA dataset NLVR. In the jointly trained bAbI-10k, we set a new state-of-the-art, achieving a mean error of less than 0.5%. Moreover, a simple ensemble of two of our models solves all 20 tasks in the joint version of the benchmark.

Approximating Likelihood Ratios with Calibrated Discriminative Classifiers

In many fields of science, generalized likelihood ratio tests are established tools for statistical inference. At the same time, it has become increasingly common that a simulator (or generative model) is used to describe complex processes that tie parameters $\theta$ of an underlying theory and measurement apparatus to high-dimensional observations $\mathbf{x}\in \mathbb{R}^p$. However, simulator often do not provide a way to evaluate the likelihood function for a given observation $\mathbf{x}$, which motivates a new class of likelihood-free inference algorithms. In this paper, we show that likelihood ratios are invariant under a specific class of dimensionality reduction maps $\mathbb{R}^p \mapsto \mathbb{R}$. As a direct consequence, we show that discriminative classifiers can be used to approximate the generalized likelihood ratio statistic when only a generative model for the data is available. This leads to a new machine learning-based approach to likelihood-free inference that is complementary to Approximate Bayesian Computation, and which does not require a prior on the model parameters. Experimental results on artificial problems with known exact likelihoods illustrate the potential of the proposed method.