Statistical Agnostic Regression: a machine learning method to validate regression models

Regression analysis is a central topic in statistical modeling, aiming to estimate the relationships between a dependent variable, commonly referred to as the response variable, and one or more independent variables, i.e., explanatory variables. Linear regression is by far the most popular method for performing this task in several fields of research, such as prediction, forecasting, or causal inference. Beyond various classical methods to solve linear regression problems, such as Ordinary Least Squares, Ridge, or Lasso regressions - which are often the foundation for more advanced machine learning (ML) techniques - the latter have been successfully applied in this scenario without a formal definition of statistical significance. At most, permutation or classical analyses based on empirical measures (e.g., residuals or accuracy) have been conducted to reflect the greater ability of ML estimations for detection. In this paper, we introduce a method, named Statistical Agnostic Regression (SAR), for evaluating the statistical significance of an ML-based linear regression based on concentration inequalities of the actual risk using the analysis of the worst case. To achieve this goal, similar to the classification problem, we define a threshold to establish that there is sufficient evidence with a probability of at least 1-eta to conclude that there is a linear relationship in the population between the explanatory (feature) and the response (label) variables. Simulations in only two dimensions demonstrate the ability of the proposed agnostic test to provide a similar analysis of variance given by the classical $F$ test for the slope parameter.

Is K-fold cross validation the best model selection method for Machine Learning?

As a technique that can compactly represent complex patterns, machine learning has significant potential for predictive inference. K-fold cross-validation (CV) is the most common approach to ascertaining the likelihood that a machine learning outcome is generated by chance and frequently outperforms conventional hypothesis testing. This improvement uses measures directly obtained from machine learning classifications, such as accuracy, that do not have a parametric description. To approach a frequentist analysis within machine learning pipelines, a permutation test or simple statistics from data partitions (i.e. folds) can be added to estimate confidence intervals. Unfortunately, neither parametric nor non-parametric tests solve the inherent problems around partitioning small sample-size datasets and learning from heterogeneous data sources. The fact that machine learning strongly depends on the learning parameters and the distribution of data across folds recapitulates familiar difficulties around excess false positives and replication. The origins of this problem are demonstrated by simulating common experimental circumstances, including small sample sizes, low numbers of predictors, and heterogeneous data sources. A novel statistical test based on K-fold CV and the Upper Bound of the actual error (K-fold CUBV) is composed, where uncertain predictions of machine learning with CV are bounded by the \emph{worst case} through the evaluation of concentration inequalities. Probably Approximately Correct-Bayesian upper bounds for linear classifiers in combination with K-fold CV is used to estimate the empirical error. The performance with neuroimaging datasets suggests this is a robust criterion for detecting effects, validating accuracy values obtained from machine learning whilst avoiding excess false positives.

Tiled sparse coding in eigenspaces for the COVID-19 diagnosis in chest X-ray images

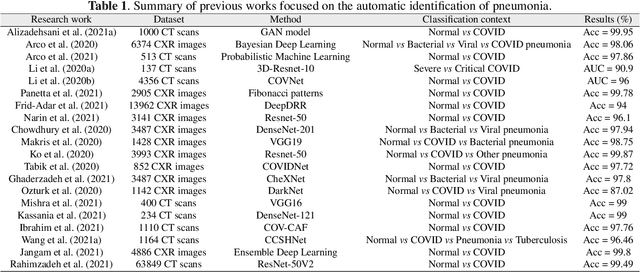
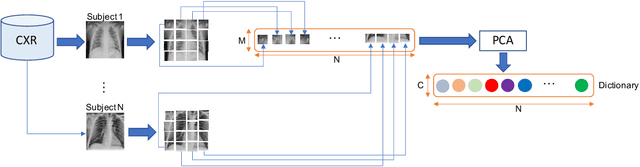
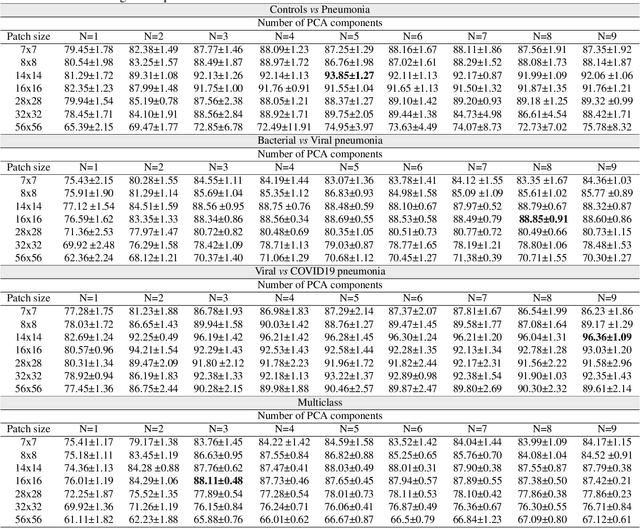
The ongoing crisis of the COVID-19 (Coronavirus disease 2019) pandemic has changed the world. According to the World Health Organization (WHO), 4 million people have died due to this disease, whereas there have been more than 180 million confirmed cases of COVID-19. The collapse of the health system in many countries has demonstrated the need of developing tools to automatize the diagnosis of the disease from medical imaging. Previous studies have used deep learning for this purpose. However, the performance of this alternative highly depends on the size of the dataset employed for training the algorithm. In this work, we propose a classification framework based on sparse coding in order to identify the pneumonia patterns associated with different pathologies. Specifically, each chest X-ray (CXR) image is partitioned into different tiles. The most relevant features extracted from PCA are then used to build the dictionary within the sparse coding procedure. Once images are transformed and reconstructed from the elements of the dictionary, classification is performed from the reconstruction errors of individual patches associated with each image. Performance is evaluated in a real scenario where simultaneously differentiation between four different pathologies: control vs bacterial pneumonia vs viral pneumonia vs COVID-19. The accuracy when identifying the presence of pneumonia is 93.85%, whereas 88.11% is obtained in the 4-class classification context. The excellent results and the pioneering use of sparse coding in this scenario evidence the applicability of this approach as an aid for clinicians in a real-world environment.