Statistical Agnostic Regression: a machine learning method to validate regression models

Regression analysis is a central topic in statistical modeling, aiming to estimate the relationships between a dependent variable, commonly referred to as the response variable, and one or more independent variables, i.e., explanatory variables. Linear regression is by far the most popular method for performing this task in several fields of research, such as prediction, forecasting, or causal inference. Beyond various classical methods to solve linear regression problems, such as Ordinary Least Squares, Ridge, or Lasso regressions - which are often the foundation for more advanced machine learning (ML) techniques - the latter have been successfully applied in this scenario without a formal definition of statistical significance. At most, permutation or classical analyses based on empirical measures (e.g., residuals or accuracy) have been conducted to reflect the greater ability of ML estimations for detection. In this paper, we introduce a method, named Statistical Agnostic Regression (SAR), for evaluating the statistical significance of an ML-based linear regression based on concentration inequalities of the actual risk using the analysis of the worst case. To achieve this goal, similar to the classification problem, we define a threshold to establish that there is sufficient evidence with a probability of at least 1-eta to conclude that there is a linear relationship in the population between the explanatory (feature) and the response (label) variables. Simulations in only two dimensions demonstrate the ability of the proposed agnostic test to provide a similar analysis of variance given by the classical $F$ test for the slope parameter.

A hypothesis-driven method based on machine learning for neuroimaging data analysis

There remains an open question about the usefulness and the interpretation of Machine learning (MLE) approaches for discrimination of spatial patterns of brain images between samples or activation states. In the last few decades, these approaches have limited their operation to feature extraction and linear classification tasks for between-group inference. In this context, statistical inference is assessed by randomly permuting image labels or by the use of random effect models that consider between-subject variability. These multivariate MLE-based statistical pipelines, whilst potentially more effective for detecting activations than hypotheses-driven methods, have lost their mathematical elegance, ease of interpretation, and spatial localization of the ubiquitous General linear Model (GLM). Recently, the estimation of the conventional GLM has been demonstrated to be connected to an univariate classification task when the design matrix is expressed as a binary indicator matrix. In this paper we explore the complete connection between the univariate GLM and MLE \emph{regressions}. To this purpose we derive a refined statistical test with the GLM based on the parameters obtained by a linear Support Vector Regression (SVR) in the \emph{inverse} problem (SVR-iGLM). Subsequently, random field theory (RFT) is employed for assessing statistical significance following a conventional GLM benchmark. Experimental results demonstrate how parameter estimations derived from each model (mainly GLM and SVR) result in different experimental design estimates that are significantly related to the predefined functional task. Moreover, using real data from a multisite initiative the proposed MLE-based inference demonstrates statistical power and the control of false positives, outperforming the regular GLM.

Uncertainty-driven ensembles of deep architectures for multiclass classification. Application to COVID-19 diagnosis in chest X-ray images

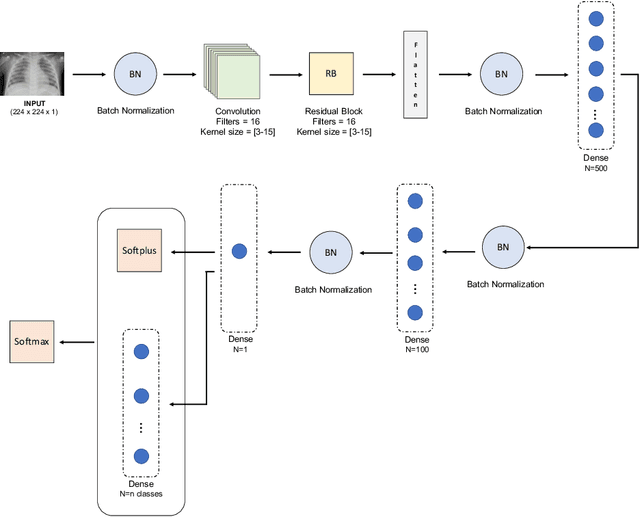
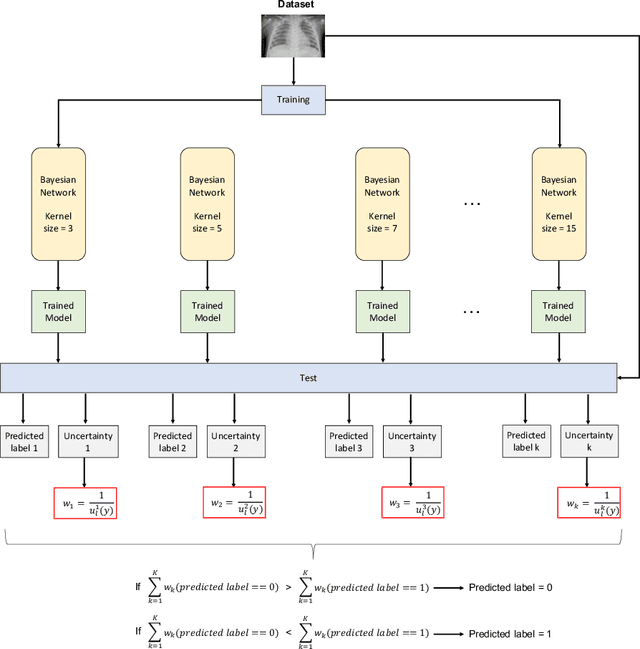
Respiratory diseases kill million of people each year. Diagnosis of these pathologies is a manual, time-consuming process that has inter and intra-observer variability, delaying diagnosis and treatment. The recent COVID-19 pandemic has demonstrated the need of developing systems to automatize the diagnosis of pneumonia, whilst Convolutional Neural Network (CNNs) have proved to be an excellent option for the automatic classification of medical images. However, given the need of providing a confidence classification in this context it is crucial to quantify the reliability of the model's predictions. In this work, we propose a multi-level ensemble classification system based on a Bayesian Deep Learning approach in order to maximize performance while quantifying the uncertainty of each classification decision. This tool combines the information extracted from different architectures by weighting their results according to the uncertainty of their predictions. Performance of the Bayesian network is evaluated in a real scenario where simultaneously differentiating between four different pathologies: control vs bacterial pneumonia vs viral pneumonia vs COVID-19 pneumonia. A three-level decision tree is employed to divide the 4-class classification into three binary classifications, yielding an accuracy of 98.06% and overcoming the results obtained by recent literature. The reduced preprocessing needed for obtaining this high performance, in addition to the information provided about the reliability of the predictions evidence the applicability of the system to be used as an aid for clinicians.

Spectral Clustering: An empirical study of Approximation Algorithms and its Application to the Attrition Problem

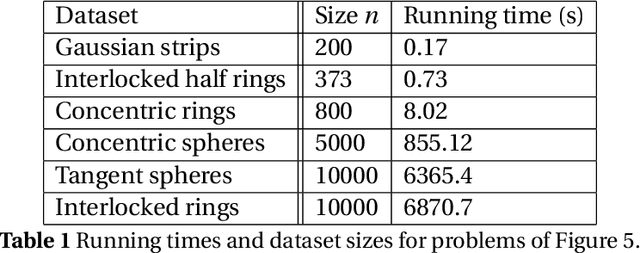
Clustering is the problem of separating a set of objects into groups (called clusters) so that objects within the same cluster are more similar to each other than to those in different clusters. Spectral clustering is a now well-known method for clustering which utilizes the spectrum of the data similarity matrix to perform this separation. Since the method relies on solving an eigenvector problem, it is computationally expensive for large datasets. To overcome this constraint, approximation methods have been developed which aim to reduce running time while maintaining accurate classification. In this article, we summarize and experimentally evaluate several approximation methods for spectral clustering. From an applications standpoint, we employ spectral clustering to solve the so-called attrition problem, where one aims to identify from a set of employees those who are likely to voluntarily leave the company from those who are not. Our study sheds light on the empirical performance of existing approximate spectral clustering methods and shows the applicability of these methods in an important business optimization related problem.