Quantification using Permutation-Invariant Networks based on Histograms

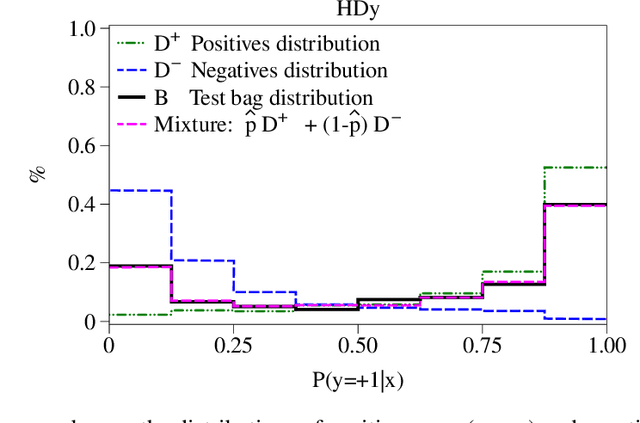
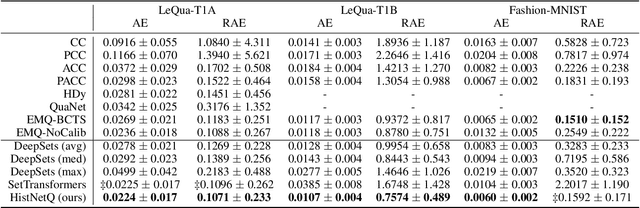
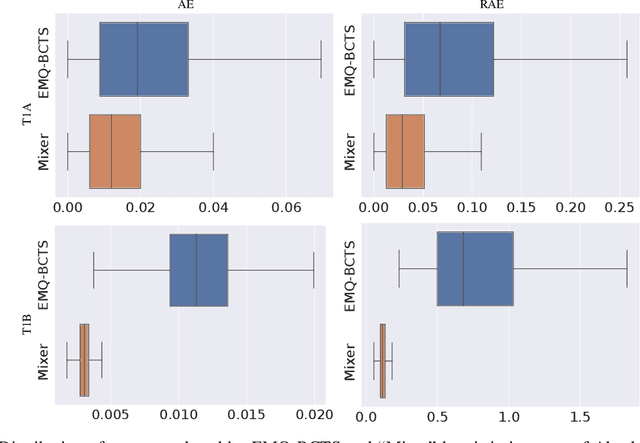
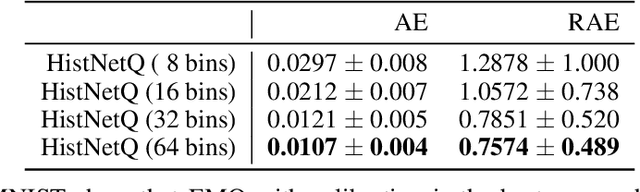
Quantification, also known as class prevalence estimation, is the supervised learning task in which a model is trained to predict the prevalence of each class in a given bag of examples. This paper investigates the application of deep neural networks to tasks of quantification in scenarios where it is possible to apply a symmetric supervised approach that eliminates the need for classification as an intermediary step, directly addressing the quantification problem. Additionally, it discusses existing permutation-invariant layers designed for set processing and assesses their suitability for quantification. In light of our analysis, we propose HistNetQ, a novel neural architecture that relies on a permutation-invariant representation based on histograms that is specially suited for quantification problems. Our experiments carried out in the only quantification competition held to date, show that HistNetQ outperforms other deep neural architectures devised for set processing, as well as the state-of-the-art quantification methods. Furthermore, HistNetQ offers two significant advantages over traditional quantification methods: i) it does not require the labels of the training examples but only the prevalence values of a collection of training bags, making it applicable to new scenarios; and ii) it is able to optimize any custom quantification-oriented loss function.

Kernel Density Estimation for Multiclass Quantification

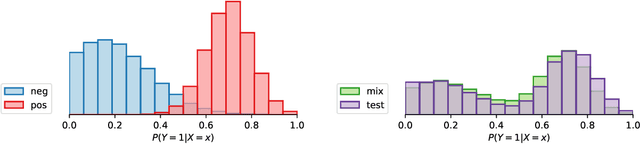
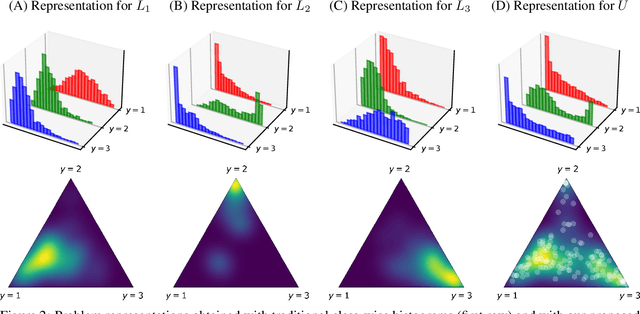
Several disciplines, like the social sciences, epidemiology, sentiment analysis, or market research, are interested in knowing the distribution of the classes in a population rather than the individual labels of the members thereof. Quantification is the supervised machine learning task concerned with obtaining accurate predictors of class prevalence, and to do so particularly in the presence of label shift. The distribution-matching (DM) approaches represent one of the most important families among the quantification methods that have been proposed in the literature so far. Current DM approaches model the involved populations by means of histograms of posterior probabilities. In this paper, we argue that their application to the multiclass setting is suboptimal since the histograms become class-specific, thus missing the opportunity to model inter-class information that may exist in the data. We propose a new representation mechanism based on multivariate densities that we model via kernel density estimation (KDE). The experiments we have carried out show our method, dubbed KDEy, yields superior quantification performance with respect to previous DM approaches. We also investigate the KDE-based representation within the maximum likelihood framework and show KDEy often shows superior performance with respect to the expectation-maximization method for quantification, arguably the strongest contender in the quantification arena to date.

Rectifying Classifier Chains for Multi-Label Classification

Classifier chains have recently been proposed as an appealing method for tackling the multi-label classification task. In addition to several empirical studies showing its state-of-the-art performance, especially when being used in its ensemble variant, there are also some first results on theoretical properties of classifier chains. Continuing along this line, we analyze the influence of a potential pitfall of the learning process, namely the discrepancy between the feature spaces used in training and testing: While true class labels are used as supplementary attributes for training the binary models along the chain, the same models need to rely on estimations of these labels at prediction time. We elucidate under which circumstances the attribute noise thus created can affect the overall prediction performance. As a result of our findings, we propose two modifications of classifier chains that are meant to overcome this problem. Experimentally, we show that our variants are indeed able to produce better results in cases where the original chaining process is likely to fail.