Quantification via Gaussian Latent Space Representations

Quantification, or prevalence estimation, is the task of predicting the prevalence of each class within an unknown bag of examples. Most existing quantification methods in the literature rely on prior probability shift assumptions to create a quantification model that uses the predictions of an underlying classifier to make optimal prevalence estimates. In this work, we present an end-to-end neural network that uses Gaussian distributions in latent spaces to obtain invariant representations of bags of examples. This approach addresses the quantification problem using deep learning, enabling the optimization of specific loss functions relevant to the problem and avoiding the need for an intermediate classifier, tackling the quantification problem as a direct optimization problem. Our method achieves state-of-the-art results, both against traditional quantification methods and other deep learning approaches for quantification. The code needed to reproduce all our experiments is publicly available at https://github.com/AICGijon/gmnet.

Quantification using Permutation-Invariant Networks based on Histograms

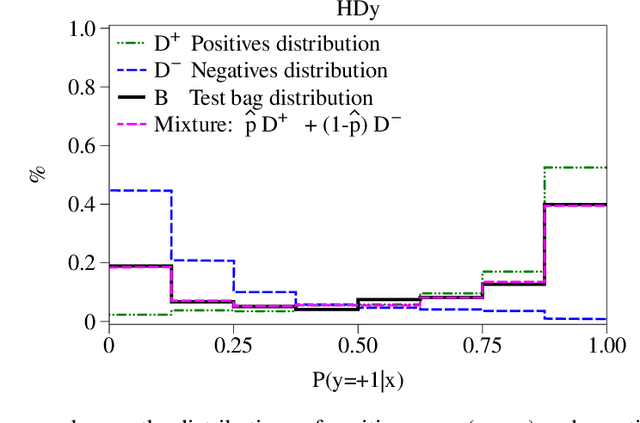
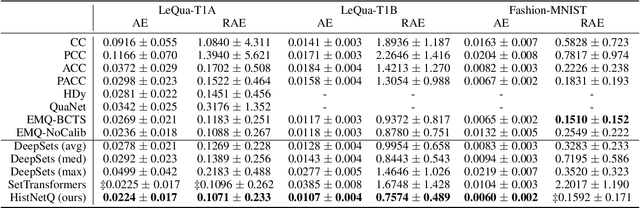
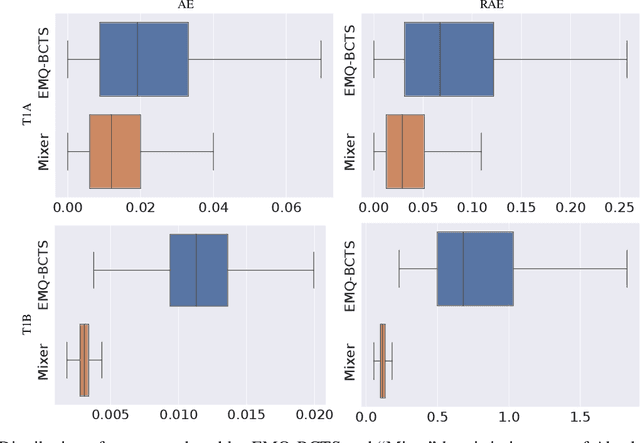
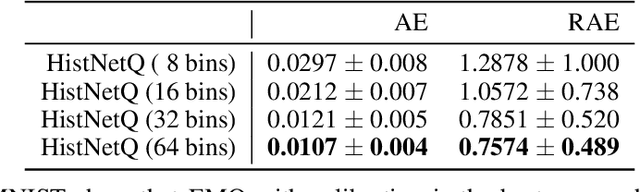
Quantification, also known as class prevalence estimation, is the supervised learning task in which a model is trained to predict the prevalence of each class in a given bag of examples. This paper investigates the application of deep neural networks to tasks of quantification in scenarios where it is possible to apply a symmetric supervised approach that eliminates the need for classification as an intermediary step, directly addressing the quantification problem. Additionally, it discusses existing permutation-invariant layers designed for set processing and assesses their suitability for quantification. In light of our analysis, we propose HistNetQ, a novel neural architecture that relies on a permutation-invariant representation based on histograms that is specially suited for quantification problems. Our experiments carried out in the only quantification competition held to date, show that HistNetQ outperforms other deep neural architectures devised for set processing, as well as the state-of-the-art quantification methods. Furthermore, HistNetQ offers two significant advantages over traditional quantification methods: i) it does not require the labels of the training examples but only the prevalence values of a collection of training bags, making it applicable to new scenarios; and ii) it is able to optimize any custom quantification-oriented loss function.

Kernel Density Estimation for Multiclass Quantification

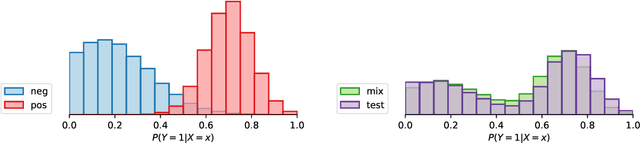
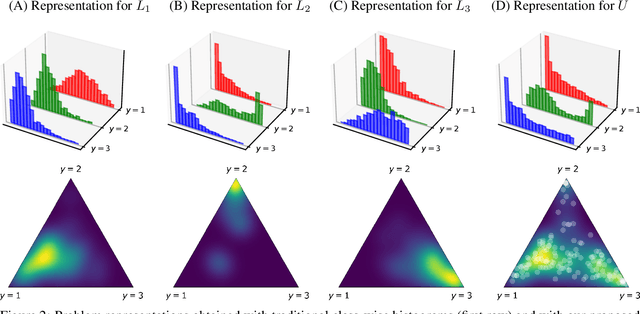
Several disciplines, like the social sciences, epidemiology, sentiment analysis, or market research, are interested in knowing the distribution of the classes in a population rather than the individual labels of the members thereof. Quantification is the supervised machine learning task concerned with obtaining accurate predictors of class prevalence, and to do so particularly in the presence of label shift. The distribution-matching (DM) approaches represent one of the most important families among the quantification methods that have been proposed in the literature so far. Current DM approaches model the involved populations by means of histograms of posterior probabilities. In this paper, we argue that their application to the multiclass setting is suboptimal since the histograms become class-specific, thus missing the opportunity to model inter-class information that may exist in the data. We propose a new representation mechanism based on multivariate densities that we model via kernel density estimation (KDE). The experiments we have carried out show our method, dubbed KDEy, yields superior quantification performance with respect to previous DM approaches. We also investigate the KDE-based representation within the maximum likelihood framework and show KDEy often shows superior performance with respect to the expectation-maximization method for quantification, arguably the strongest contender in the quantification arena to date.

Binary Quantification and Dataset Shift: An Experimental Investigation

Quantification is the supervised learning task that consists of training predictors of the class prevalence values of sets of unlabelled data, and is of special interest when the labelled data on which the predictor has been trained and the unlabelled data are not IID, i.e., suffer from dataset shift. To date, quantification methods have mostly been tested only on a special case of dataset shift, i.e., prior probability shift; the relationship between quantification and other types of dataset shift remains, by and large, unexplored. In this work we carry out an experimental analysis of how current quantification algorithms behave under different types of dataset shift, in order to identify limitations of current approaches and hopefully pave the way for the development of more broadly applicable methods. We do this by proposing a fine-grained taxonomy of types of dataset shift, by establishing protocols for the generation of datasets affected by these types of shift, and by testing existing quantification methods on the datasets thus generated. One finding that results from this investigation is that many existing quantification methods that had been found robust to prior probability shift are not necessarily robust to other types of dataset shift. A second finding is that no existing quantification method seems to be robust enough to dealing with all the types of dataset shift we simulate in our experiments. The code needed to reproduce all our experiments is publicly available at https://github.com/pglez82/quant_datasetshift.