Juan Fernández-Olivares
A Roadmap to Guide the Integration of LLMs in Hierarchical Planning
Jan 14, 2025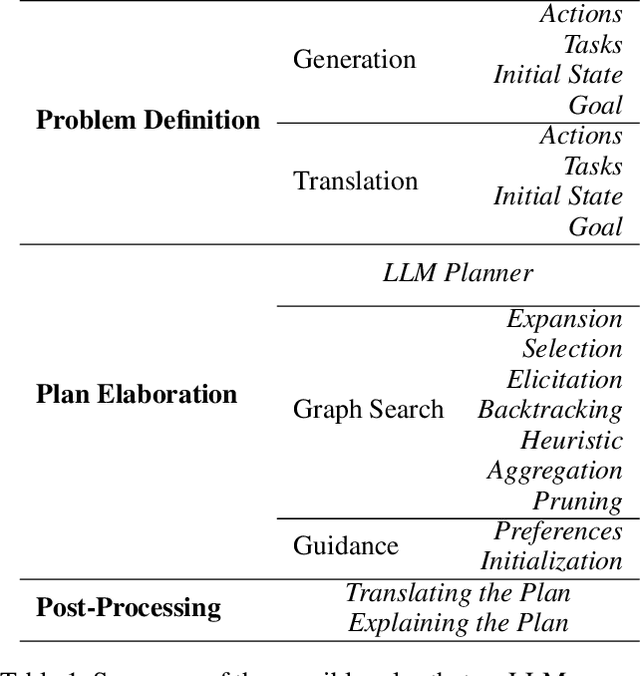
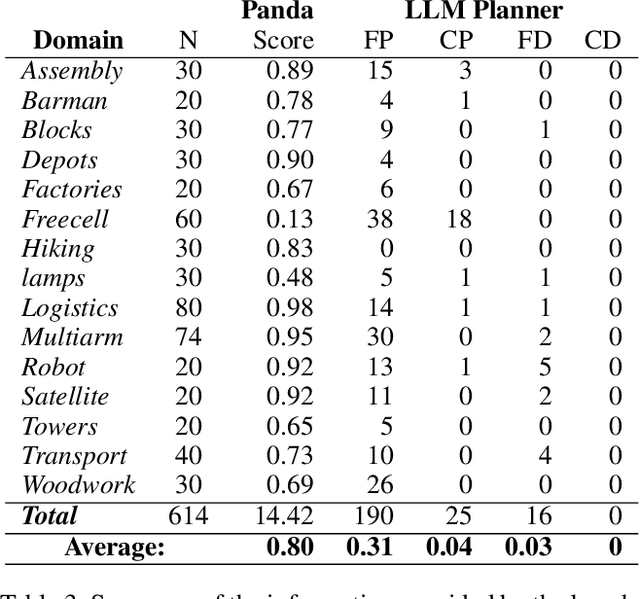
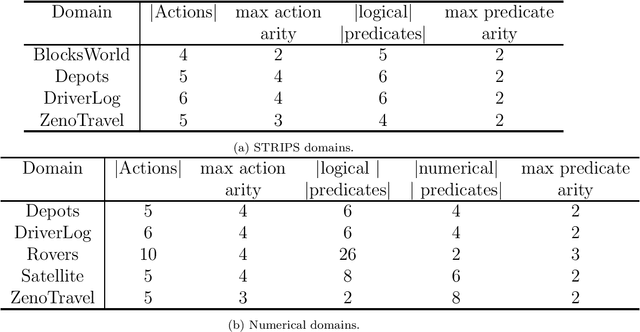
Abstract:Recent advances in Large Language Models (LLMs) are fostering their integration into several reasoning-related fields, including Automated Planning (AP). However, their integration into Hierarchical Planning (HP), a subfield of AP that leverages hierarchical knowledge to enhance planning performance, remains largely unexplored. In this preliminary work, we propose a roadmap to address this gap and harness the potential of LLMs for HP. To this end, we present a taxonomy of integration methods, exploring how LLMs can be utilized within the HP life cycle. Additionally, we provide a benchmark with a standardized dataset for evaluating the performance of future LLM-based HP approaches, and present initial results for a state-of-the-art HP planner and LLM planner. As expected, the latter exhibits limited performance (3\% correct plans, and none with a correct hierarchical decomposition) but serves as a valuable baseline for future approaches.
Learning to Select Goals in Automated Planning with Deep-Q Learning
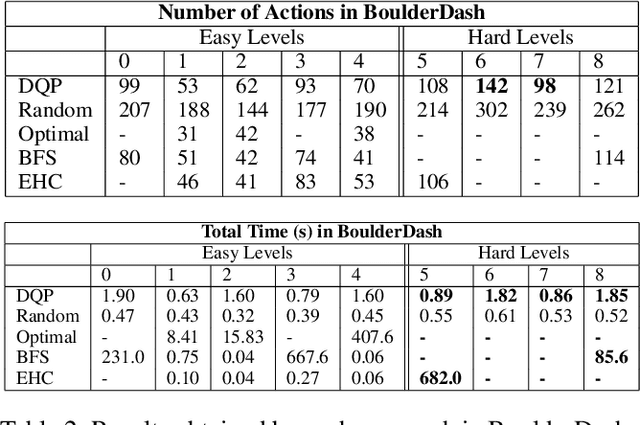
Jun 20, 2024Abstract:In this work we propose a planning and acting architecture endowed with a module which learns to select subgoals with Deep Q-Learning. This allows us to decrease the load of a planner when faced with scenarios with real-time restrictions. We have trained this architecture on a video game environment used as a standard test-bed for intelligent systems applications, testing it on different levels of the same game to evaluate its generalization abilities. We have measured the performance of our approach as more training data is made available, as well as compared it with both a state-of-the-art, classical planner and the standard Deep Q-Learning algorithm. The results obtained show our model performs better than the alternative methods considered, when both plan quality (plan length) and time requirements are taken into account. On the one hand, it is more sample-efficient than standard Deep Q-Learning, and it is able to generalize better across levels. On the other hand, it reduces problem-solving time when compared with a state-of-the-art automated planner, at the expense of obtaining plans with only 9% more actions.
* 25 pages, 4 figures
Towards a Unified Framework for Sequential Decision Making
Oct 03, 2023Abstract:In recent years, the integration of Automated Planning (AP) and Reinforcement Learning (RL) has seen a surge of interest. To perform this integration, a general framework for Sequential Decision Making (SDM) would prove immensely useful, as it would help us understand how AP and RL fit together. In this preliminary work, we attempt to provide such a framework, suitable for any method ranging from Classical Planning to Deep RL, by drawing on concepts from Probability Theory and Bayesian inference. We formulate an SDM task as a set of training and test Markov Decision Processes (MDPs), to account for generalization. We provide a general algorithm for SDM which we hypothesize every SDM method is based on. According to it, every SDM algorithm can be seen as a procedure that iteratively improves its solution estimate by leveraging the task knowledge available. Finally, we derive a set of formulas and algorithms for calculating interesting properties of SDM tasks and methods, which make possible their empirical evaluation and comparison.
A Review of Symbolic, Subsymbolic and Hybrid Methods for Sequential Decision Making
Apr 20, 2023
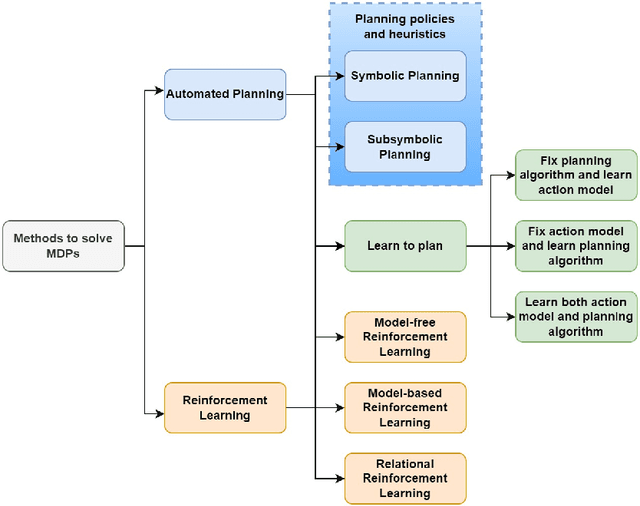
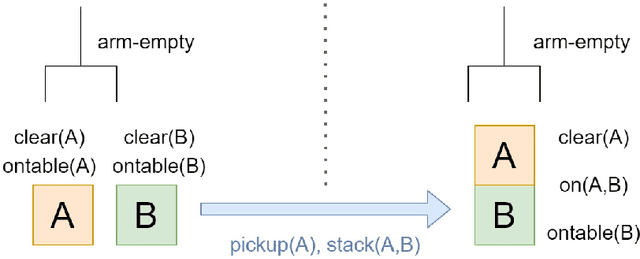
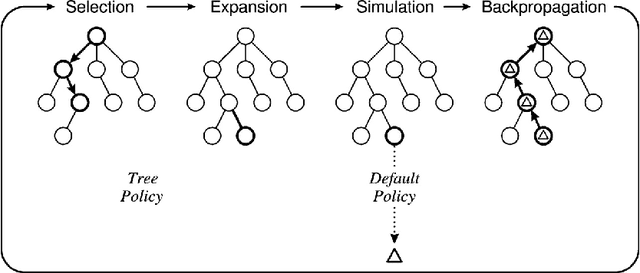
Abstract:The field of Sequential Decision Making (SDM) provides tools for solving Sequential Decision Processes (SDPs), where an agent must make a series of decisions in order to complete a task or achieve a goal. Historically, two competing SDM paradigms have view for supremacy. Automated Planning (AP) proposes to solve SDPs by performing a reasoning process over a model of the world, often represented symbolically. Conversely, Reinforcement Learning (RL) proposes to learn the solution of the SDP from data, without a world model, and represent the learned knowledge subsymbolically. In the spirit of reconciliation, we provide a review of symbolic, subsymbolic and hybrid methods for SDM. We cover both methods for solving SDPs (e.g., AP, RL and techniques that learn to plan) and for learning aspects of their structure (e.g., world models, state invariants and landmarks). To the best of our knowledge, no other review in the field provides the same scope. As an additional contribution, we discuss what properties an ideal method for SDM should exhibit and argue that neurosymbolic AI is the current approach which most closely resembles this ideal method. Finally, we outline several proposals to advance the field of SDM via the integration of symbolic and subsymbolic AI.
NeSIG: A Neuro-Symbolic Method for Learning to Generate Planning Problems
Jan 24, 2023Abstract:In the field of Automated Planning there is often the need for a set of planning problems from a particular domain, e.g., to be used as training data for Machine Learning or as benchmarks in planning competitions. In most cases, these problems are created either by hand or by a domain-specific generator, putting a burden on the human designers. In this paper we propose NeSIG, to the best of our knowledge the first domain-independent method for automatically generating planning problems that are valid, diverse and difficult to solve. We formulate problem generation as a Markov Decision Process and train two generative policies with Deep Reinforcement Learning to generate problems with the desired properties. We conduct experiments on several classical domains, comparing our method with handcrafted domain-specific generators that generate valid and diverse problems but do not optimize difficulty. The results show NeSIG is able to automatically generate valid problems of greater difficulty than the competitor approaches, while maintaining good diversity.
Learning Numerical Action Models from Noisy Input Data
Nov 09, 2021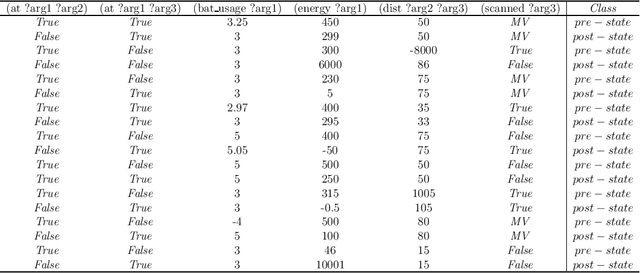
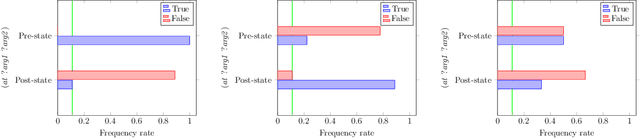
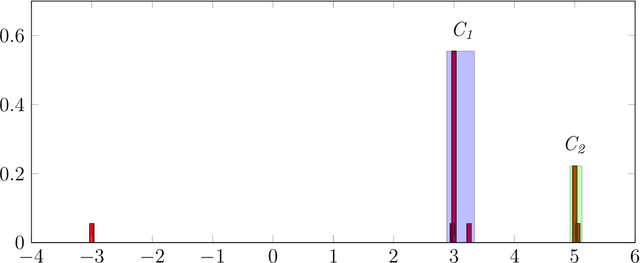
Abstract:This paper presents the PlanMiner-N algorithm, a domain learning technique based on the PlanMiner domain learning algorithm. The algorithm presented here improves the learning capabilities of PlanMiner when using noisy data as input. The PlanMiner algorithm is able to infer arithmetic and logical expressions to learn numerical planning domains from the input data, but it was designed to work under situations of incompleteness making it unreliable when facing noisy input data. In this paper, we propose a series of enhancements to the learning process of PlanMiner to expand its capabilities to learn from noisy data. These methods preprocess the input data by detecting noise and filtering it and study the learned action models learned to find erroneous preconditions/effects in them. The methods proposed in this paper were tested using a set of domains from the International Planning Competition (IPC). The results obtained indicate that PlanMiner-N improves the performance of PlanMiner greatly when facing noisy input data.
Goal Reasoning by Selecting Subgoals with Deep Q-Learning
Dec 22, 2020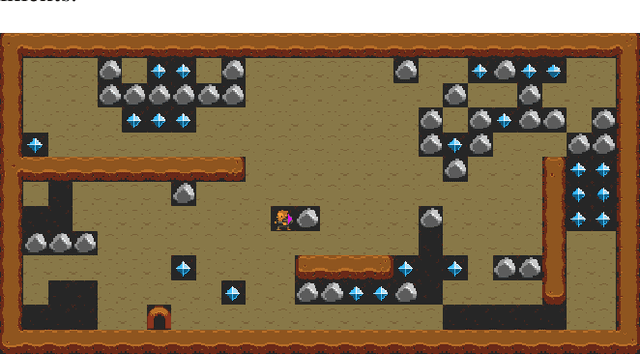

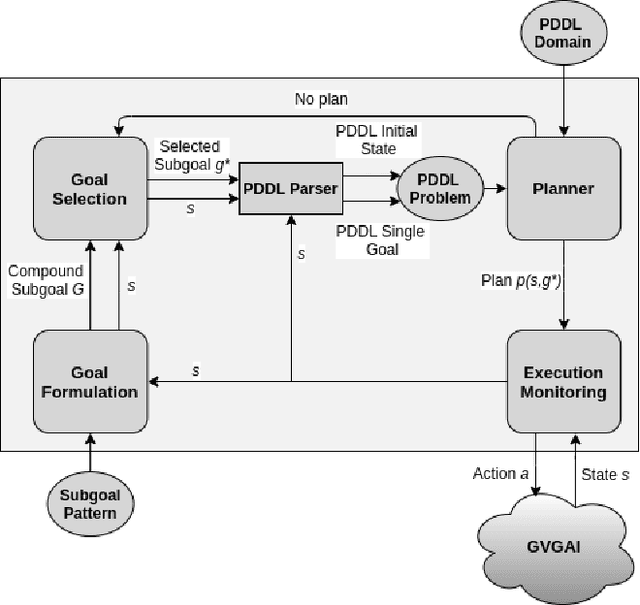
Abstract:In this work we propose a goal reasoning method which learns to select subgoals with Deep Q-Learning in order to decrease the load of a planner when faced with scenarios with tight time restrictions, such as online execution systems. We have designed a CNN-based goal selection module and trained it on a standard video game environment, testing it on different games (planning domains) and levels (planning problems) to measure its generalization abilities. When comparing its performance with a satisfying planner, the results obtained show both approaches are able to find plans of good quality, but our method greatly decreases planning time. We conclude our approach can be successfully applied to different types of domains (games), and shows good generalization properties when evaluated on new levels (problems) of the same game (domain).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge