An Efficient Algorithm for Multiple-Pursuer-Multiple-Evader Pursuit/Evasion Game

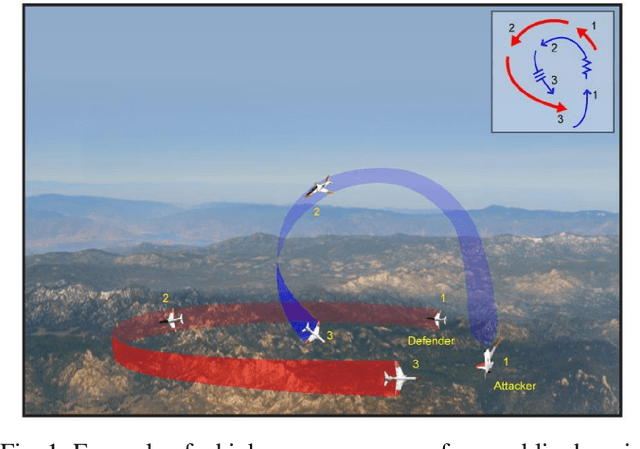
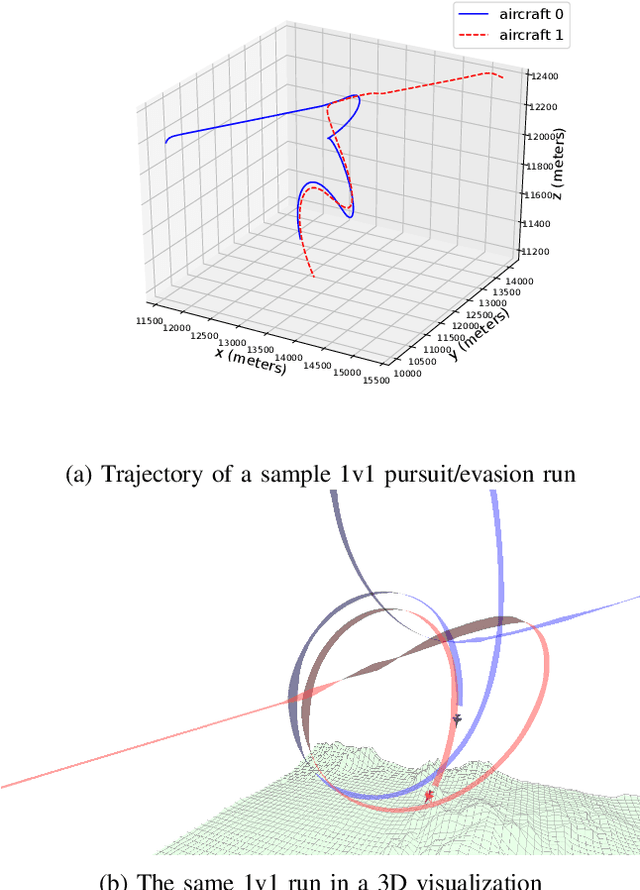
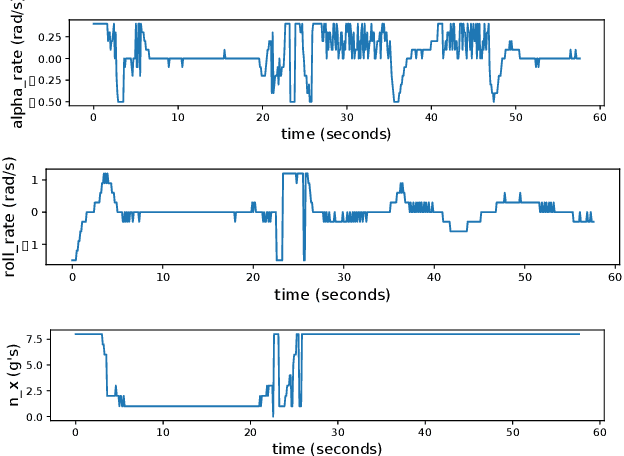
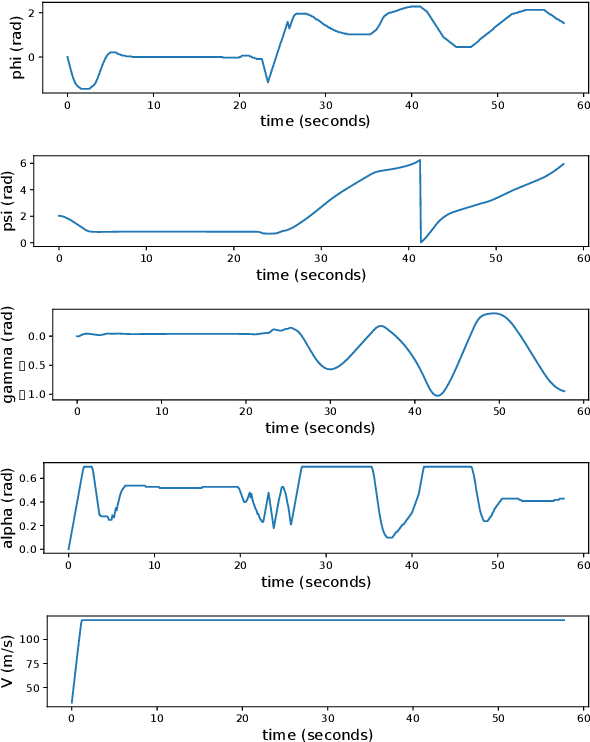
We present a method for pursuit/evasion that is highly efficient and and scales to large teams of aircraft. The underlying algorithm is an efficient algorithm for solving Markov Decision Processes (MDPs) that supports fully continuous state spaces. We demonstrate the algorithm in a team pursuit/evasion setting in a 3D environment using a pseudo-6DOF model and study performance by varying sizes of team members. We show that as the number of aircraft in the simulation grows, computational performance remains efficient and is suitable for real-time systems. We also define probability-to-win and survivability metrics that describe the teams' performance over multiple trials, and show that the algorithm performs consistently. We provide numerical results showing control inputs for a typical 1v1 encounter and provide videos for 1v1, 2v2, 3v3, 4v4, and 10v10 contests to demonstrate the ability of the algorithm to adapt seamlessly to complex environments.

Memoryless Exact Solutions for Deterministic MDPs with Sparse Rewards

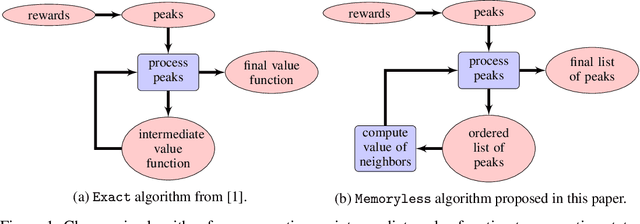
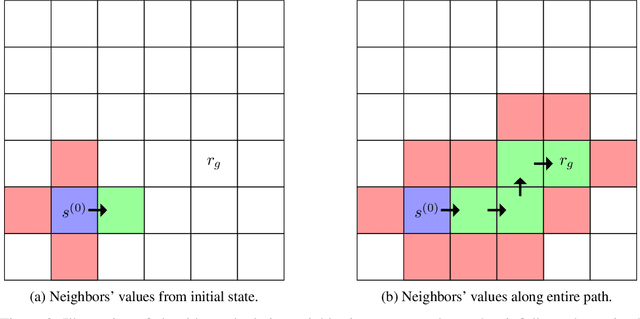
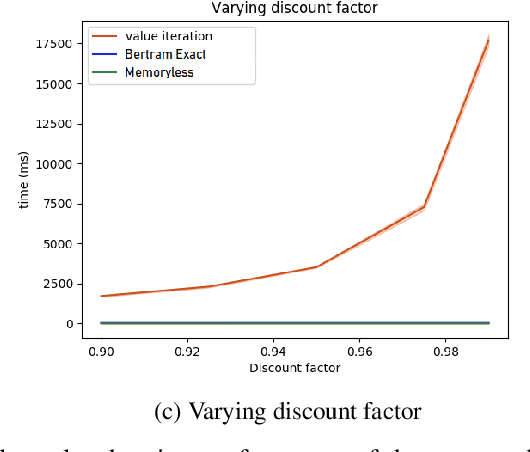
We propose an algorithm for deterministic continuous Markov Decision Processes with sparse rewards that computes the optimal policy exactly with no dependency on the size of the state space. The algorithm has time complexity of $O( |R|^3 \times |A|^2 )$ and memory complexity of $O( |R| \times |A| )$, where $|R|$ is the number of reward sources and $|A|$ is the number of actions. Furthermore, we describe a companion algorithm that can follow the optimal policy from any initial state without computing the entire value function, instead computing on-demand the value of states as they are needed. The algorithm to solve the MDP does not depend on the size of the state space for either time or memory complexity, and the ability to follow the optimal policy is linear in time and space with the path length of following the optimal policy from the initial state. We demonstrate the algorithm operation side by side with value iteration on tractable MDPs.

Fast Online Exact Solutions for Deterministic MDPs with Sparse Rewards

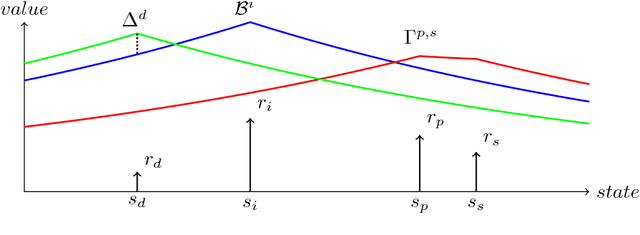
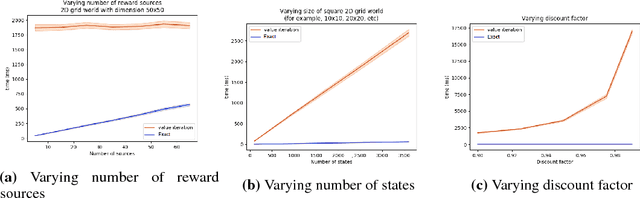
Markov Decision Processes (MDPs) are a mathematical framework for modeling sequential decision making under uncertainty. The classical approaches for solving MDPs are well known and have been widely studied, some of which rely on approximation techniques to solve MDPs with large state space and/or action space. However, most of these classical solution approaches and their approximation techniques still take much computation time to converge and usually must be re-computed if the reward function is changed. This paper introduces a novel alternative approach for exactly and efficiently solving deterministic, continuous MDPs with sparse reward sources. When the environment is such that the "distance" between states can be determined in constant time, e.g. grid world, our algorithm offers $O( |R|^2 \times |A|^2 \times |S|)$, where $|R|$ is the number of reward sources, $|A|$ is the number of actions, and $|S|$ is the number of states. Memory complexity for the algorithm is $O( |S| + |R| \times |A|)$. This new approach opens new avenues for boosting computational performance for certain classes of MDPs and is of tremendous value for MDP applications such as robotics and unmanned systems. This paper describes the algorithm and presents numerical experiment results to demonstrate its powerful computational performance. We also provide rigorous mathematical description of the approach.