Memoryless Exact Solutions for Deterministic MDPs with Sparse Rewards
Paper and Code
May 17, 2018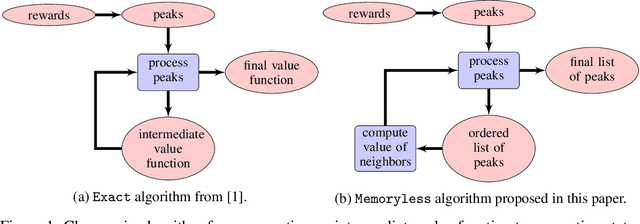
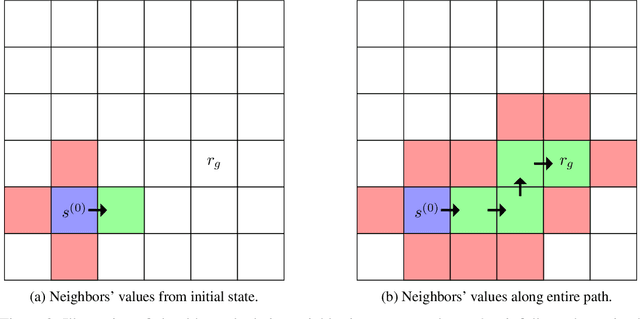
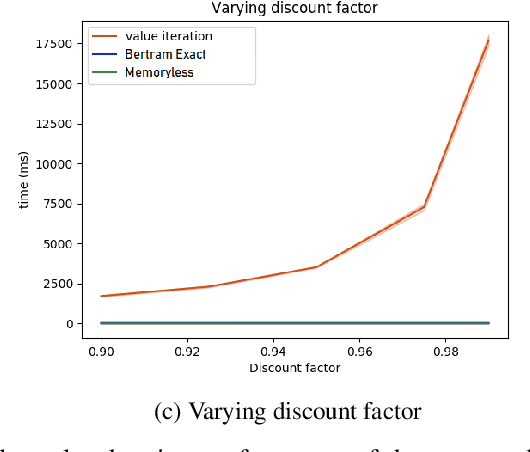
We propose an algorithm for deterministic continuous Markov Decision Processes with sparse rewards that computes the optimal policy exactly with no dependency on the size of the state space. The algorithm has time complexity of $O( |R|^3 \times |A|^2 )$ and memory complexity of $O( |R| \times |A| )$, where $|R|$ is the number of reward sources and $|A|$ is the number of actions. Furthermore, we describe a companion algorithm that can follow the optimal policy from any initial state without computing the entire value function, instead computing on-demand the value of states as they are needed. The algorithm to solve the MDP does not depend on the size of the state space for either time or memory complexity, and the ability to follow the optimal policy is linear in time and space with the path length of following the optimal policy from the initial state. We demonstrate the algorithm operation side by side with value iteration on tractable MDPs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge