Interpretable (not just posthoc-explainable) heterogeneous survivor bias-corrected treatment effects for assignment of postdischarge interventions to prevent readmissions

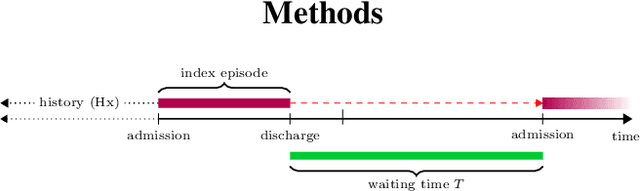
We used survival analysis to quantify the impact of postdischarge evaluation and management (E/M) services in preventing hospital readmission or death. Our approach avoids a specific pitfall of applying machine learning to this problem, which is an inflated estimate of the effect of interventions, due to survivors bias -- where the magnitude of inflation may be conditional on heterogeneous confounders in the population. This bias arises simply because in order to receive an intervention after discharge, a person must not have been readmitted in the intervening period. After deriving an expression for this phantom effect, we controlled for this and other biases within an inherently interpretable Bayesian survival framework. We identified case management services as being the most impactful for reducing readmissions overall, particularly for patients discharged to long term care facilities, with high resource utilization in the quarter preceding admission.

Interpretable (not just posthoc-explainable) medical claims modeling for discharge placement to prevent avoidable all-cause readmissions or death

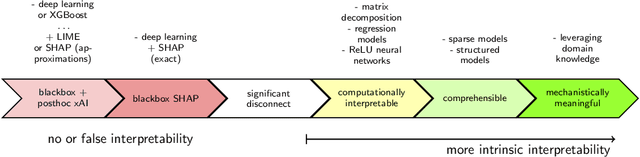
This manuscript addresses the simultaneous problems of predicting all-cause inpatient readmission or death after discharge, and quantifying the impact of discharge placement in preventing these adverse events. To this end, we developed an inherently interpretable multilevel Bayesian modeling framework inspired by the piecewise linearity of ReLU-activated deep neural networks. In a survival model, we explicitly adjust for confounding in quantifying local average treatment effects for discharge placement interventions. We trained the model on a 5% sample of Medicare beneficiaries from 2008 and 2011, and then tested the model on 2012 claims. Evaluated on classification accuracy for 30-day all-cause unplanned readmissions (defined using official CMS methodology) or death, the model performed similarly against XGBoost, logistic regression (after feature engineering), and a Bayesian deep neural network trained on the same data. Tested on the 30-day classification task of predicting readmissions or death using left-out future data, the model achieved an AUROC of approximately 0.76 and and AUPRC of approximately 0.50 (relative to an overall positively rate in the testing data of 18%), demonstrating how one need not sacrifice interpretability for accuracy. Additionally, the model had a testing AUROC of 0.78 on the classification of 90-day all-cause unplanned readmission or death. We easily peer into our inherently interpretable model, summarizing its main findings. Additionally, we demonstrate how the black-box posthoc explainer tool SHAP generates explanations that are not supported by the fitted model -- and if taken at face value does not offer enough context to make a model actionable.

Sparse encoding for more-interpretable feature-selecting representations in probabilistic matrix factorization

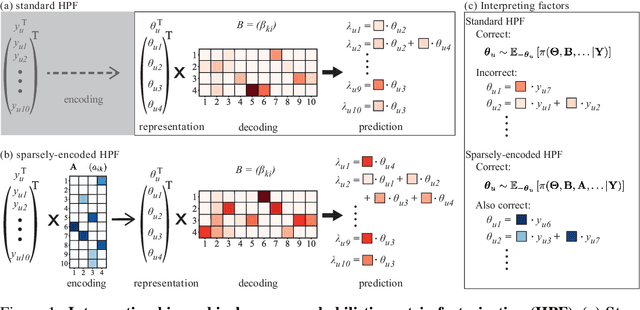
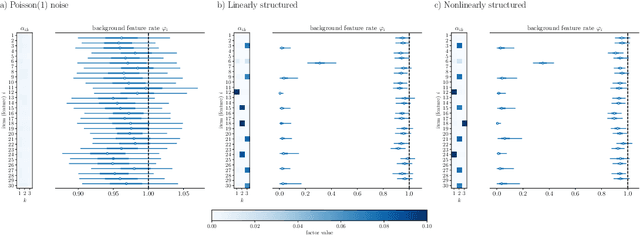
Dimensionality reduction methods for count data are critical to a wide range of applications in medical informatics and other fields where model interpretability is paramount. For such data, hierarchical Poisson matrix factorization (HPF) and other sparse probabilistic non-negative matrix factorization (NMF) methods are considered to be interpretable generative models. They consist of sparse transformations for decoding their learned representations into predictions. However, sparsity in representation decoding does not necessarily imply sparsity in the encoding of representations from the original data features. HPF is often incorrectly interpreted in the literature as if it possesses encoder sparsity. The distinction between decoder sparsity and encoder sparsity is subtle but important. Due to the lack of encoder sparsity, HPF does not possess the column-clustering property of classical NMF -- the factor loading matrix does not sufficiently define how each factor is formed from the original features. We address this deficiency by self-consistently enforcing encoder sparsity, using a generalized additive model (GAM), thereby allowing one to relate each representation coordinate to a subset of the original data features. In doing so, the method also gains the ability to perform feature selection. We demonstrate our method on simulated data and give an example of how encoder sparsity is of practical use in a concrete application of representing inpatient comorbidities in Medicare patients.

Probabilistically-autoencoded horseshoe-disentangled multidomain item-response theory models

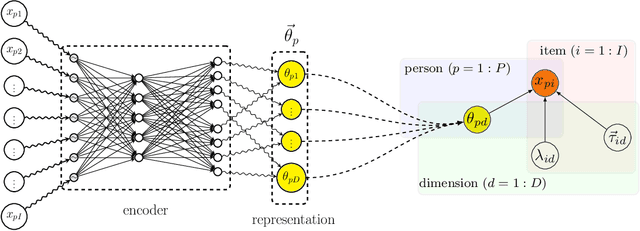
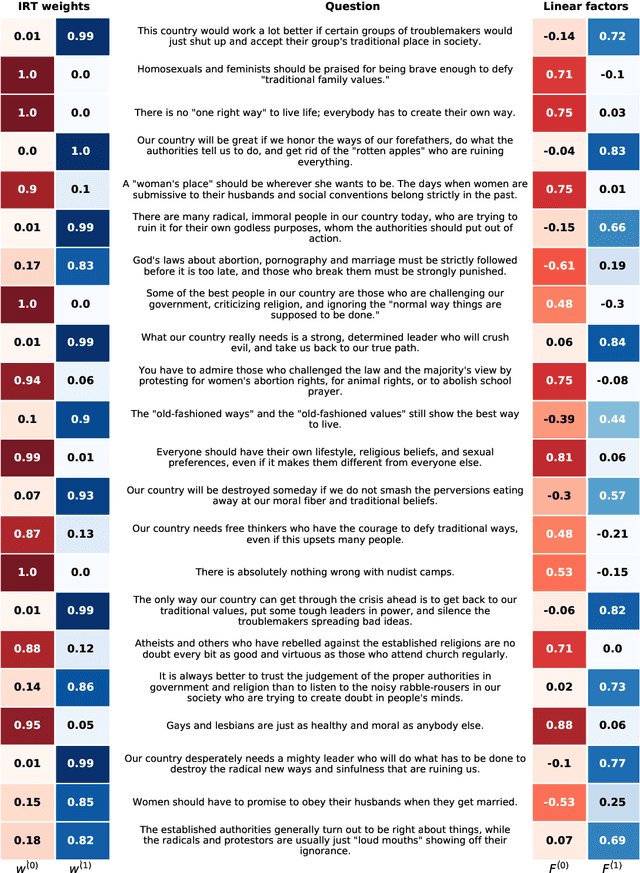
Item response theory (IRT) is a non-linear generative probabilistic paradigm for using exams to identify, quantify, and compare latent traits of individuals, relative to their peers, within a population of interest. In pre-existing multidimensional IRT methods, one requires a factorization of the test items. For this task, linear exploratory factor analysis is used, making IRT a posthoc model. We propose skipping the initial factor analysis by using a sparsity-promoting horseshoe prior to perform factorization directly within the IRT model so that all training occurs in a single self-consistent step. Being a hierarchical Bayesian model, we adapt the WAIC to the problem of dimensionality selection. IRT models are analogous to probabilistic autoencoders. By binding the generative IRT model to a Bayesian neural network (forming a probabilistic autoencoder), one obtains a scoring algorithm consistent with the interpretable Bayesian model. In some IRT applications the black-box nature of a neural network scoring machine is desirable. In this manuscript, we demonstrate within-IRT factorization and comment on scoring approaches.

Determination of hysteresis in finite-state random walks using Bayesian cross validation

Consider the problem of modeling hysteresis for finite-state random walks using higher-order Markov chains. This Letter introduces a Bayesian framework to determine, from data, the number of prior states of recent history upon which a trajectory is statistically dependent. The general recommendation is to use leave-one-out cross validation, using an easily-computable formula that is provided in closed form. Importantly, Bayes factors using flat model priors are biased in favor of too-complex a model (more hysteresis) when a large amount of data is present and the Akaike information criterion (AIC) is biased in favor of too-sparse a model (less hysteresis) when few data are present.

Iterative graph cuts for image segmentation with a nonlinear statistical shape prior

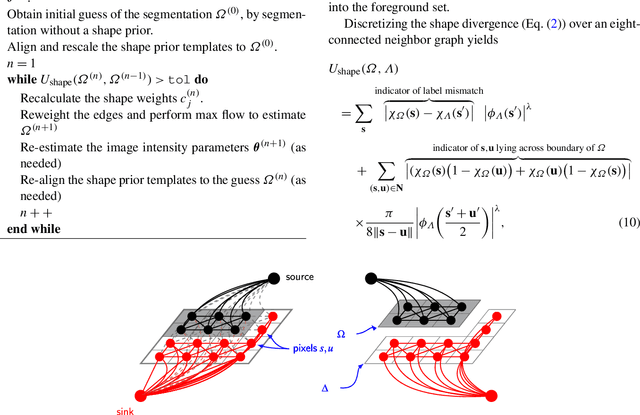
Shape-based regularization has proven to be a useful method for delineating objects within noisy images where one has prior knowledge of the shape of the targeted object. When a collection of possible shapes is available, the specification of a shape prior using kernel density estimation is a natural technique. Unfortunately, energy functionals arising from kernel density estimation are of a form that makes them impossible to directly minimize using efficient optimization algorithms such as graph cuts. Our main contribution is to show how one may recast the energy functional into a form that is minimizable iteratively and efficiently using graph cuts.