Probabilistically-autoencoded horseshoe-disentangled multidomain item-response theory models
Paper and Code
Dec 05, 2019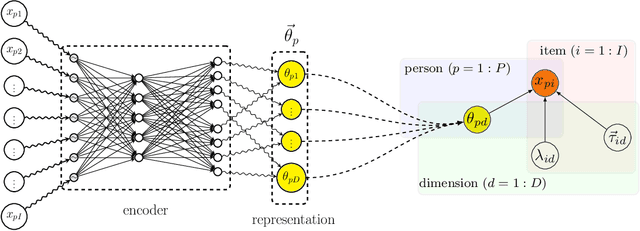
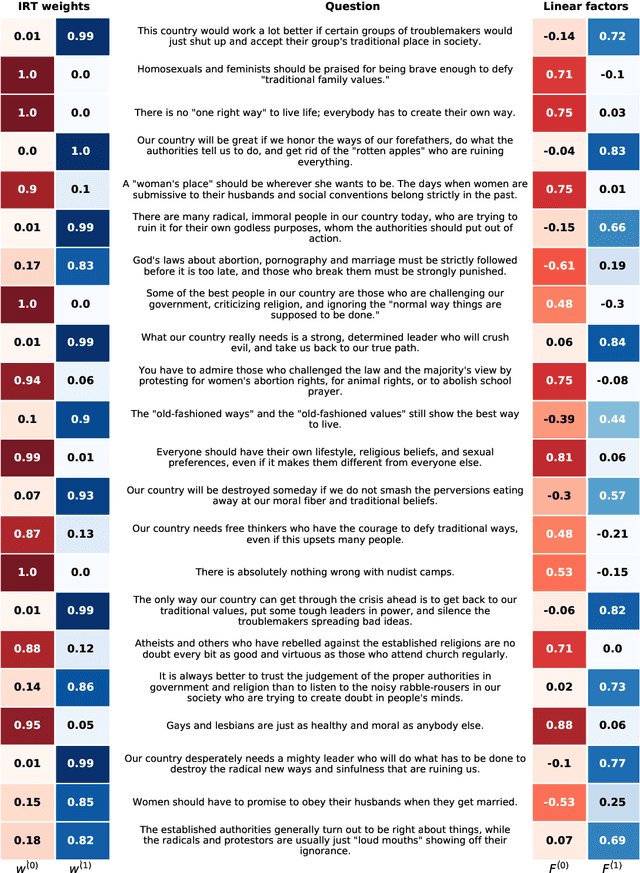

Item response theory (IRT) is a non-linear generative probabilistic paradigm for using exams to identify, quantify, and compare latent traits of individuals, relative to their peers, within a population of interest. In pre-existing multidimensional IRT methods, one requires a factorization of the test items. For this task, linear exploratory factor analysis is used, making IRT a posthoc model. We propose skipping the initial factor analysis by using a sparsity-promoting horseshoe prior to perform factorization directly within the IRT model so that all training occurs in a single self-consistent step. Being a hierarchical Bayesian model, we adapt the WAIC to the problem of dimensionality selection. IRT models are analogous to probabilistic autoencoders. By binding the generative IRT model to a Bayesian neural network (forming a probabilistic autoencoder), one obtains a scoring algorithm consistent with the interpretable Bayesian model. In some IRT applications the black-box nature of a neural network scoring machine is desirable. In this manuscript, we demonstrate within-IRT factorization and comment on scoring approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge