Statistical Mechanics of Dynamical System Identification

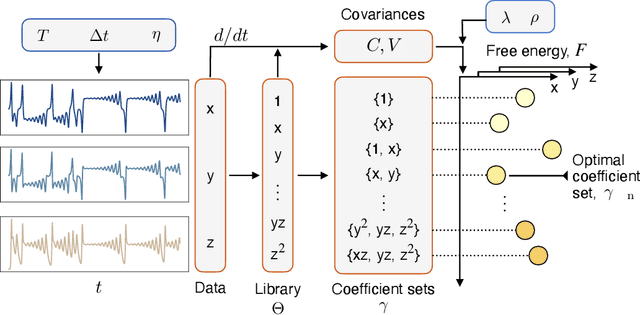
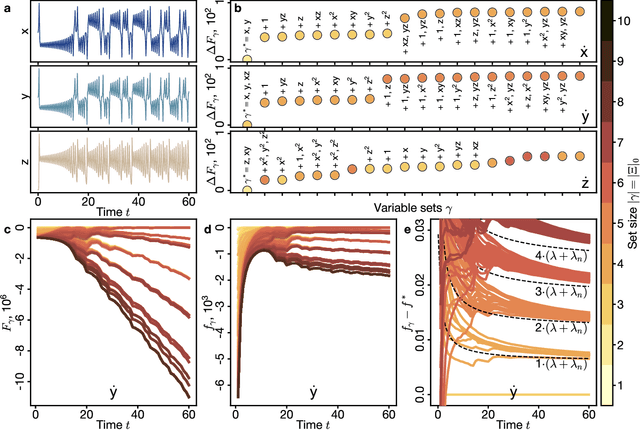
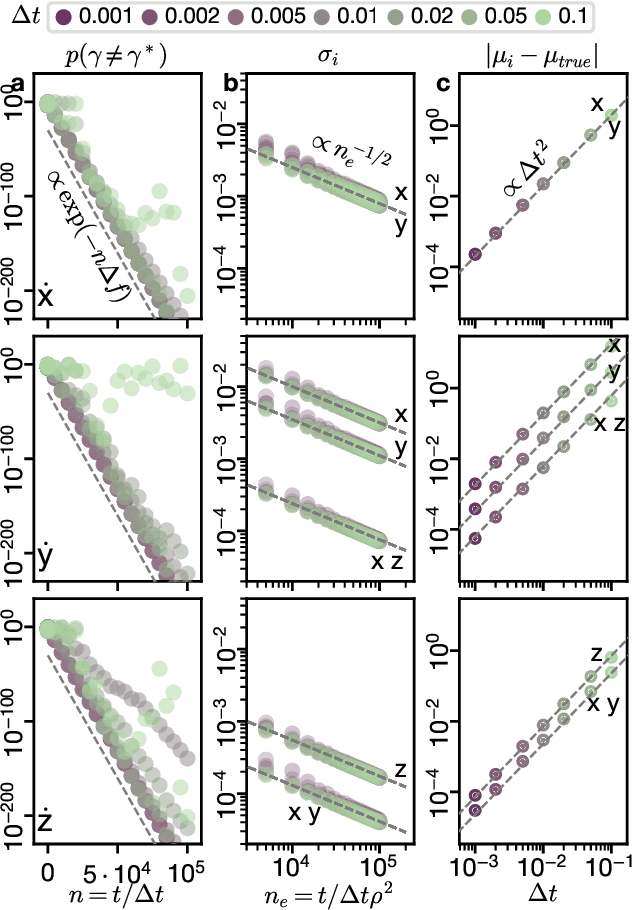
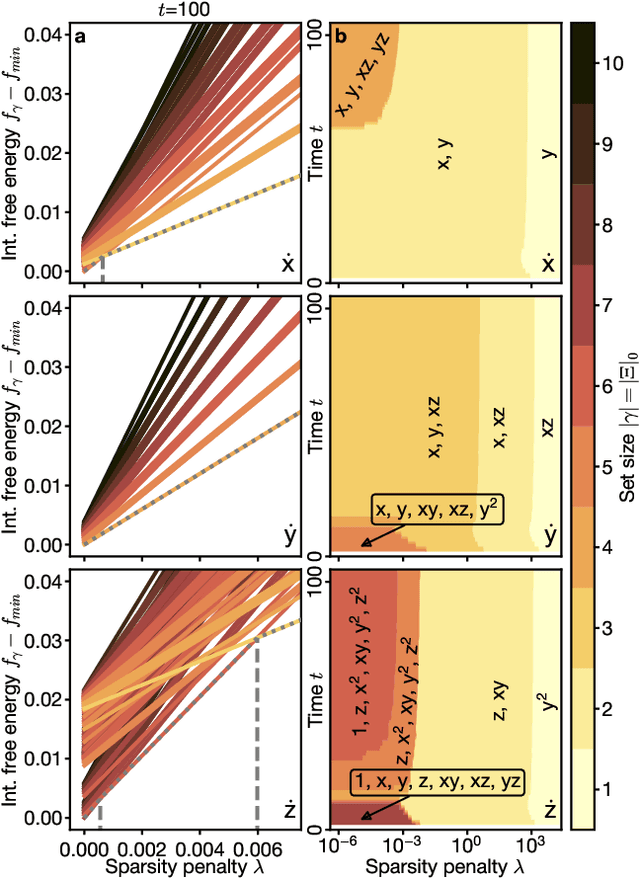
Recovering dynamical equations from observed noisy data is the central challenge of system identification. We develop a statistical mechanical approach to analyze sparse equation discovery algorithms, which typically balance data fit and parsimony through a trial-and-error selection of hyperparameters. In this framework, statistical mechanics offers tools to analyze the interplay between complexity and fitness, in analogy to that done between entropy and energy. To establish this analogy, we define the optimization procedure as a two-level Bayesian inference problem that separates variable selection from coefficient values and enables the computation of the posterior parameter distribution in closed form. A key advantage of employing statistical mechanical concepts, such as free energy and the partition function, is in the quantification of uncertainty, especially in in the low-data limit; frequently encountered in real-world applications. As the data volume increases, our approach mirrors the thermodynamic limit, leading to distinct sparsity- and noise-induced phase transitions that delineate correct from incorrect identification. This perspective of sparse equation discovery, is versatile and can be adapted to various other equation discovery algorithms.

Dimensionally Consistent Learning with Buckingham Pi

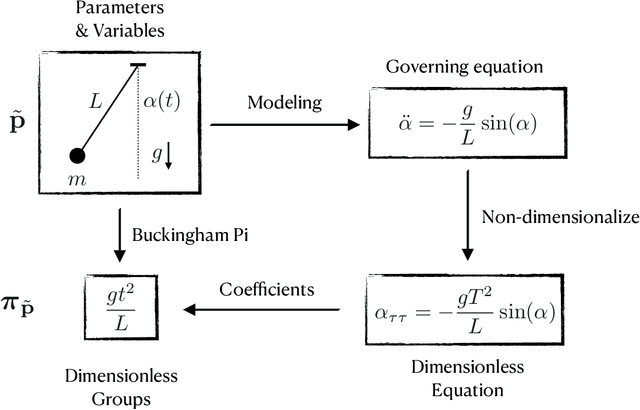
In the absence of governing equations, dimensional analysis is a robust technique for extracting insights and finding symmetries in physical systems. Given measurement variables and parameters, the Buckingham Pi theorem provides a procedure for finding a set of dimensionless groups that spans the solution space, although this set is not unique. We propose an automated approach using the symmetric and self-similar structure of available measurement data to discover the dimensionless groups that best collapse this data to a lower dimensional space according to an optimal fit. We develop three data-driven techniques that use the Buckingham Pi theorem as a constraint: (i) a constrained optimization problem with a non-parametric input-output fitting function, (ii) a deep learning algorithm (BuckiNet) that projects the input parameter space to a lower dimension in the first layer, and (iii) a technique based on sparse identification of nonlinear dynamics (SINDy) to discover dimensionless equations whose coefficients parameterize the dynamics. We explore the accuracy, robustness and computational complexity of these methods as applied to three example problems: a bead on a rotating hoop, a laminar boundary layer, and Rayleigh-B\'enard convection.

Discovering Governing Equations from Partial Measurements with Deep Delay Autoencoders

A central challenge in data-driven model discovery is the presence of hidden, or latent, variables that are not directly measured but are dynamically important. Takens' theorem provides conditions for when it is possible to augment these partial measurements with time delayed information, resulting in an attractor that is diffeomorphic to that of the original full-state system. However, the coordinate transformation back to the original attractor is typically unknown, and learning the dynamics in the embedding space has remained an open challenge for decades. Here, we design a custom deep autoencoder network to learn a coordinate transformation from the delay embedded space into a new space where it is possible to represent the dynamics in a sparse, closed form. We demonstrate this approach on the Lorenz, R\"ossler, and Lotka-Volterra systems, learning dynamics from a single measurement variable. As a challenging example, we learn a Lorenz analogue from a single scalar variable extracted from a video of a chaotic waterwheel experiment. The resulting modeling framework combines deep learning to uncover effective coordinates and the sparse identification of nonlinear dynamics (SINDy) for interpretable modeling. Thus, we show that it is possible to simultaneously learn a closed-form model and the associated coordinate system for partially observed dynamics.

Data-Driven Discovery of Coarse-Grained Equations

We introduce a general method for learning probability density function (PDF) equations from Monte Carlo simulations of partial differential equations with uncertain (random) parameters and forcings. The method relies on sparse linear regression to discover the relevant terms in the PDF equation. Unlike other methods for equation discovery, our approach accounts for salient properties of PDF equations, such as positivity, smoothness and conservation. Our results reveal a promising direction for data-driven discovery of coarse-grained PDEs in general.

Machine Learning for a Music Glove Instrument

A music glove instrument equipped with force sensitive, flex and IMU sensors is trained on an electric piano to learn note sequences based on a time series of sensor inputs. Once trained, the glove is used on any surface to generate the sequence of notes most closely related to the hand motion. The data is collected manually by a performer wearing the glove and playing on an electric keyboard. The feature space is designed to account for the key hand motion, such as the thumb-under movement. Logistic regression along with bayesian belief networks are used learn the transition probabilities from one note to another. This work demonstrates a data-driven approach for digital musical instruments in general.