From STLS to Projection-based Dictionary Selection in Sparse Regression for System Identification

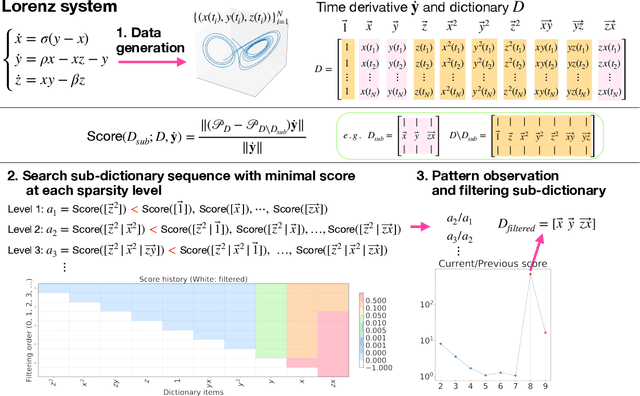
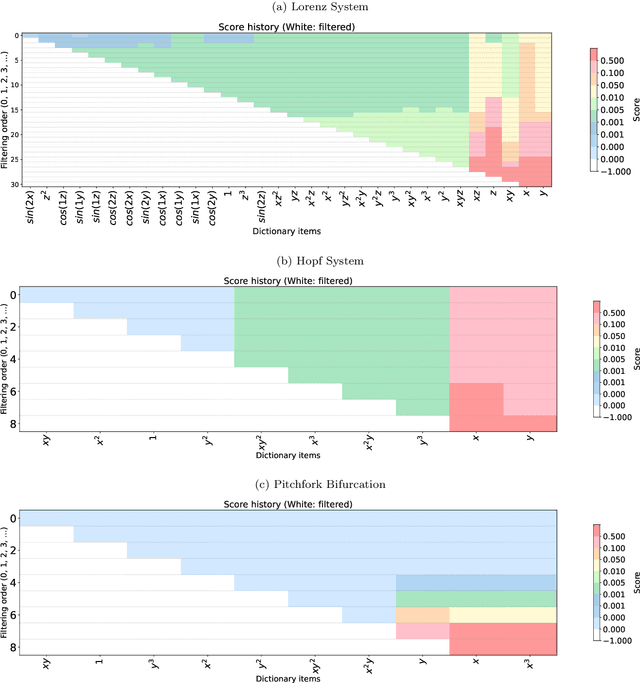
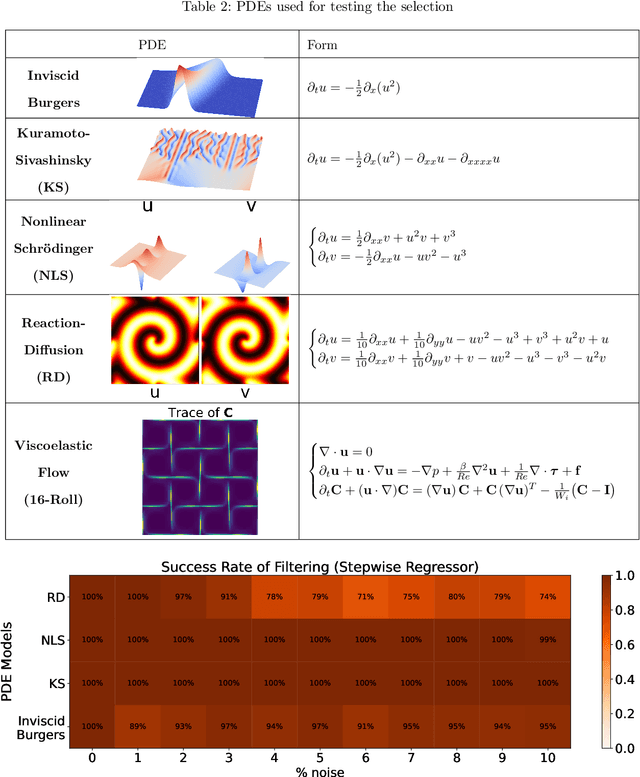
In this work, we revisit dictionary-based sparse regression, in particular, Sequential Threshold Least Squares (STLS), and propose a score-guided library selection to provide practical guidance for data-driven modeling, with emphasis on SINDy-type algorithms. STLS is an algorithm to solve the $\ell_0$ sparse least-squares problem, which relies on splitting to efficiently solve the least-squares portion while handling the sparse term via proximal methods. It produces coefficient vectors whose components depend on both the projected reconstruction errors, here referred to as the scores, and the mutual coherence of dictionary terms. The first contribution of this work is a theoretical analysis of the score and dictionary-selection strategy. This could be understood in both the original and weak SINDy regime. Second, numerical experiments on ordinary and partial differential equations highlight the effectiveness of score-based screening, improving both accuracy and interpretability in dynamical system identification. These results suggest that integrating score-guided methods to refine the dictionary more accurately may help SINDy users in some cases to enhance their robustness for data-driven discovery of governing equations.

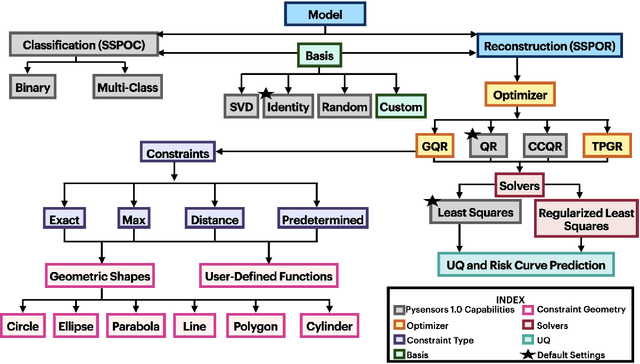
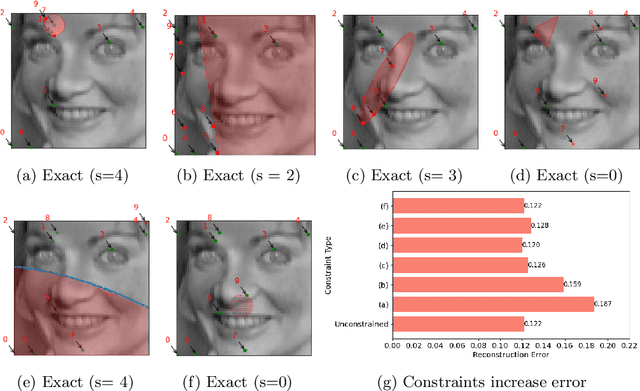
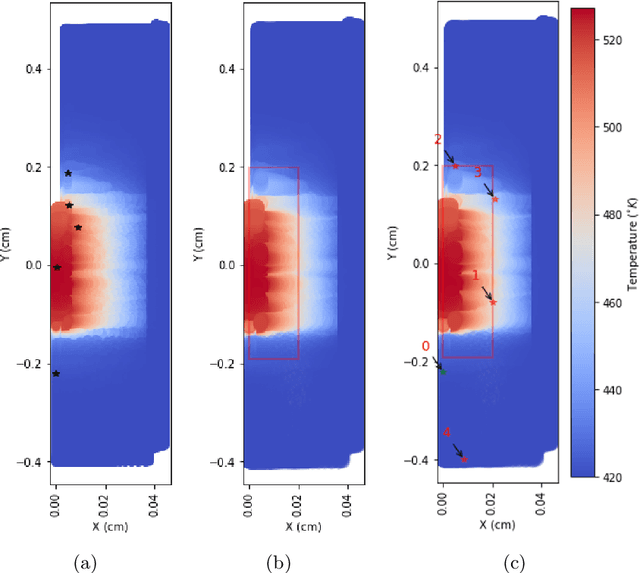
PySensors 2.0: A Python Package for Sparse Sensor Placement

PySensors is a Python package for selecting and placing a sparse set of sensors for reconstruction and classification tasks. In this major update to \texttt{PySensors}, we introduce spatially constrained sensor placement capabilities, allowing users to enforce constraints such as maximum or exact sensor counts in specific regions, incorporate predetermined sensor locations, and maintain minimum distances between sensors. We extend functionality to support custom basis inputs, enabling integration of any data-driven or spectral basis. We also propose a thermodynamic approach that goes beyond a single ``optimal'' sensor configuration and maps the complete landscape of sensor interactions induced by the training data. This comprehensive view facilitates integration with external selection criteria and enables assessment of sensor replacement impacts. The new optimization technique also accounts for over- and under-sampling of sensors, utilizing a regularized least squares approach for robust reconstruction. Additionally, we incorporate noise-induced uncertainty quantification of the estimation error and provide visual uncertainty heat maps to guide deployment decisions. To highlight these additions, we provide a brief description of the mathematical algorithms and theory underlying these new capabilities. We demonstrate the usage of new features with illustrative code examples and include practical advice for implementation across various application domains. Finally, we outline a roadmap of potential extensions to further enhance the package's functionality and applicability to emerging sensing challenges.

Statistical Mechanics of Dynamical System Identification

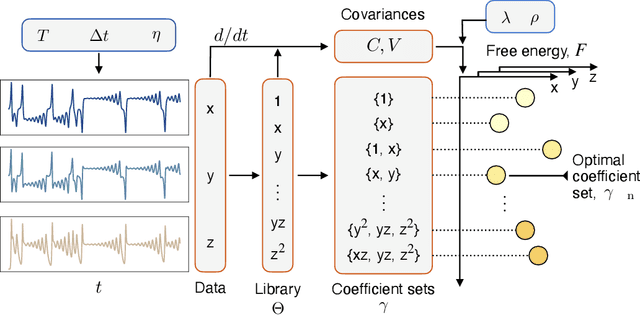
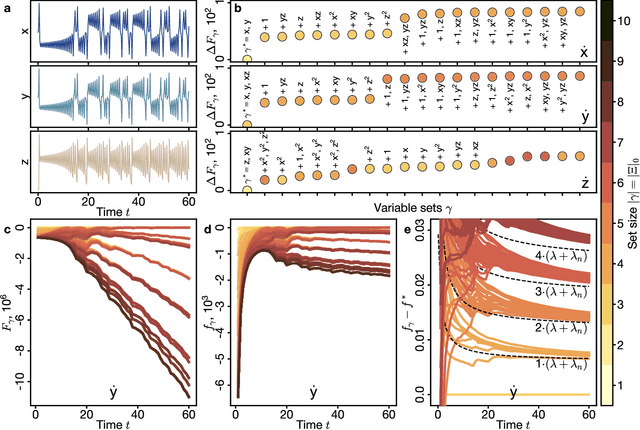
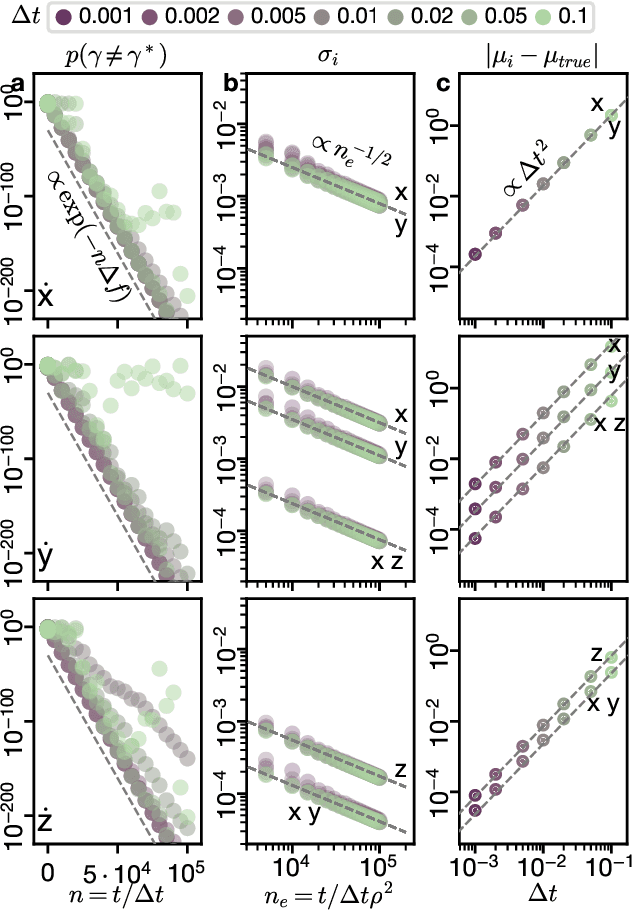
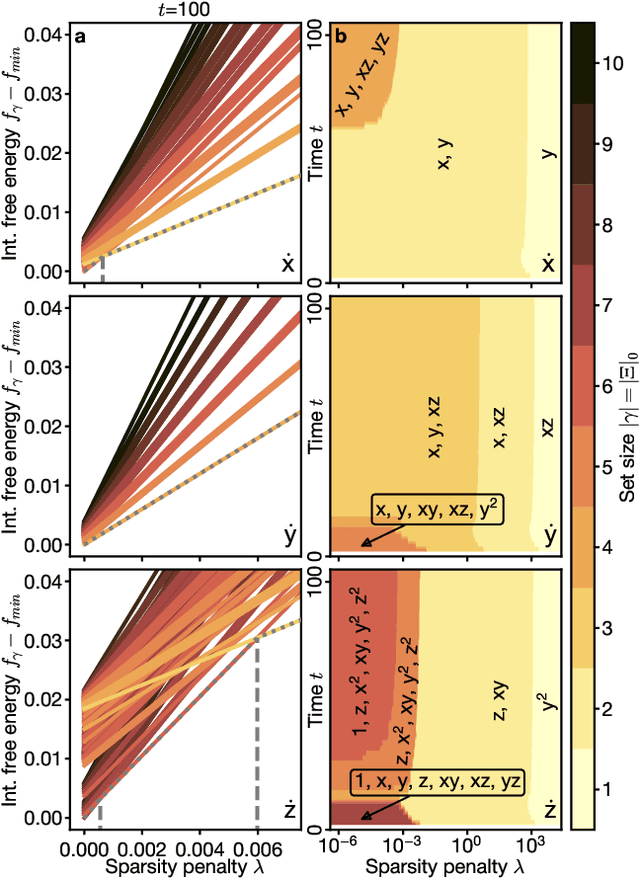
Recovering dynamical equations from observed noisy data is the central challenge of system identification. We develop a statistical mechanical approach to analyze sparse equation discovery algorithms, which typically balance data fit and parsimony through a trial-and-error selection of hyperparameters. In this framework, statistical mechanics offers tools to analyze the interplay between complexity and fitness, in analogy to that done between entropy and energy. To establish this analogy, we define the optimization procedure as a two-level Bayesian inference problem that separates variable selection from coefficient values and enables the computation of the posterior parameter distribution in closed form. A key advantage of employing statistical mechanical concepts, such as free energy and the partition function, is in the quantification of uncertainty, especially in in the low-data limit; frequently encountered in real-world applications. As the data volume increases, our approach mirrors the thermodynamic limit, leading to distinct sparsity- and noise-induced phase transitions that delineate correct from incorrect identification. This perspective of sparse equation discovery, is versatile and can be adapted to various other equation discovery algorithms.

Data-Induced Interactions of Sparse Sensors

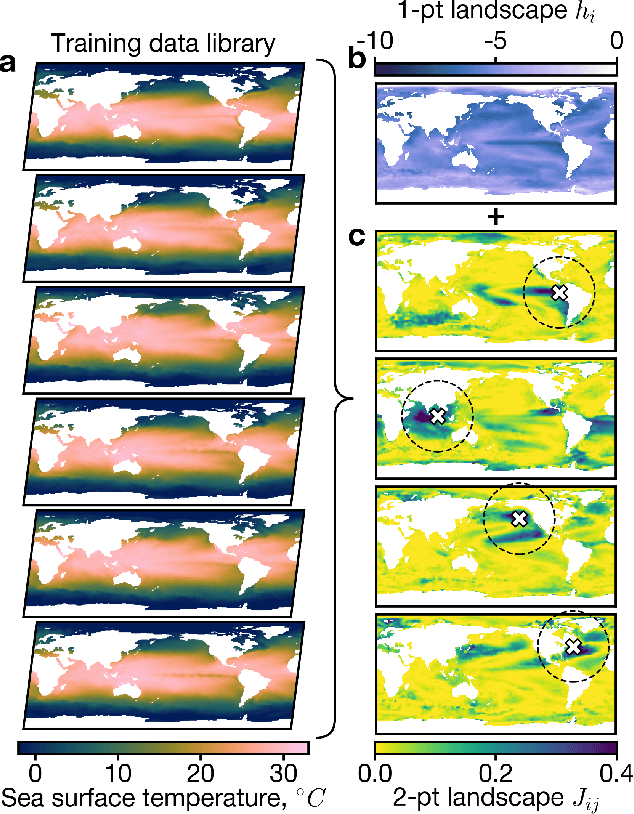
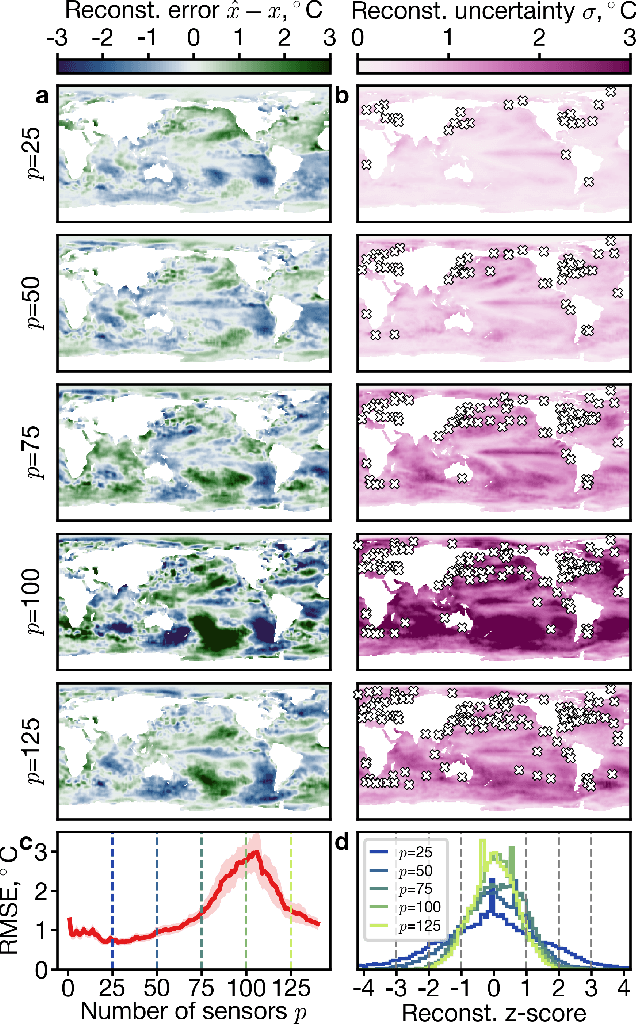
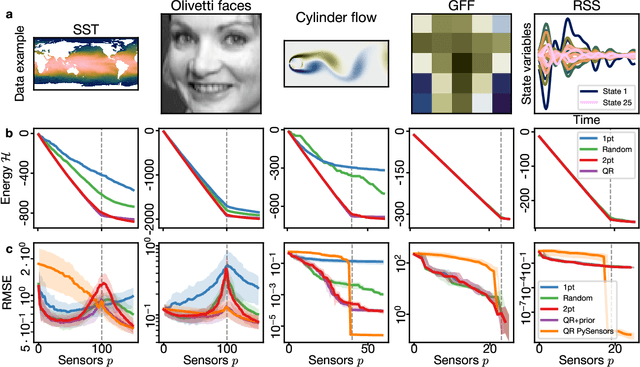
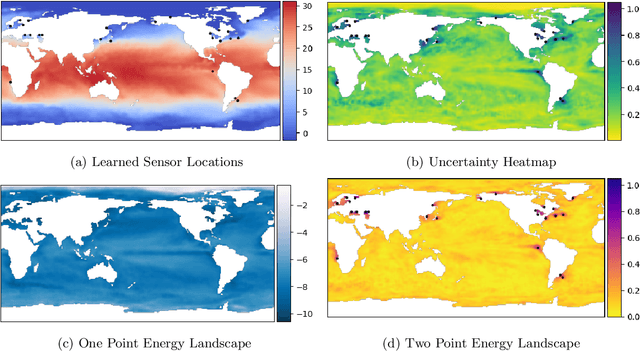
Large-dimensional empirical data in science and engineering frequently has low-rank structure and can be represented as a combination of just a few eigenmodes. Because of this structure, we can use just a few spatially localized sensor measurements to reconstruct the full state of a complex system. The quality of this reconstruction, especially in the presence of sensor noise, depends significantly on the spatial configuration of the sensors. Multiple algorithms based on gappy interpolation and QR factorization have been proposed to optimize sensor placement. Here, instead of an algorithm that outputs a singular "optimal" sensor configuration, we take a thermodynamic view to compute the full landscape of sensor interactions induced by the training data. The landscape takes the form of the Ising model in statistical physics, and accounts for both the data variance captured at each sensor location and the crosstalk between sensors. Mapping out these data-induced sensor interactions allows combining them with external selection criteria and anticipating sensor replacement impacts.