Machine Learning's Dropout Training is Distributionally Robust Optimal

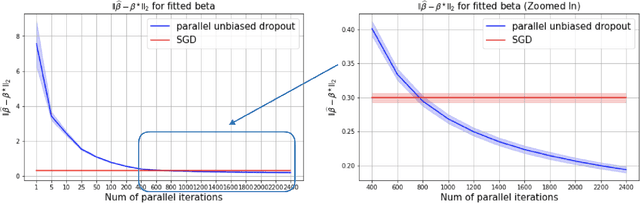
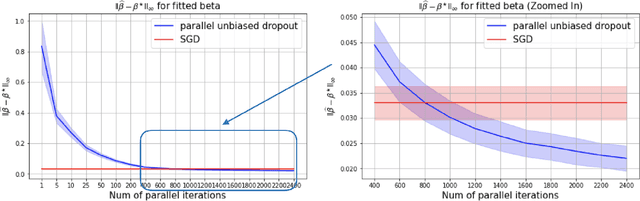
This paper shows that dropout training in Generalized Linear Models is the minimax solution of a two-player, zero-sum game where an adversarial nature corrupts a statistician's covariates using a multiplicative nonparametric errors-in-variables model. In this game---known as a Distributionally Robust Optimization problem---nature's least favorable distribution is dropout noise, where nature independently deletes entries of the covariate vector with some fixed probability $\delta$. Our decision-theoretic analysis shows that dropout training---the statistician's minimax strategy in the game---indeed provides out-of-sample expected loss guarantees for distributions that arise from multiplicative perturbations of in-sample data. This paper also provides a novel, parallelizable, Unbiased Multi-Level Monte Carlo algorithm to speed-up the implementation of dropout training. Our algorithm has a much smaller computational cost compared to the naive implementation of dropout, provided the number of data points is much smaller than the dimension of the covariate vector.

Competing Models

Different agents compete to predict a variable of interest related to a set of covariates via an unknown data generating process. All agents are Bayesian, but may consider different subsets of covariates to make their prediction. After observing a common dataset, who has the highest confidence in her predictive ability? We characterize it and show that it crucially depends on the size of the dataset. With small data, typically it is an agent using a model that is `small-dimensional,' in the sense of considering fewer covariates than the true data generating process. With big data, it is instead typically `large-dimensional,' possibly using more variables than the true model. These features are reminiscent of model selection techniques used in statistics and machine learning. However, here model selection does not emerge normatively, but positively as the outcome of competition between standard Bayesian decision makers. The theory is applied to auctions of assets where bidders observe the same information but hold different priors.